1. Геометрия
  2. В треугольнике АВС АВ =

В треугольнике АВС АВ = 3 см, ВС =2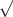\sqrt2 .Внешний угол при вершине В равен 45°. Найдите длину АС.

Zender111 Zender111    1   17.12.2020 16:17    24

Ответы
spurdosparde228 spurdosparde228  16.01.2021 16:17

Угол ОВС+угол АВС=180°, так как это смежные углы. Следовательно угол АВС=180°–угол ОВС=180°–45°=135°

\cos(135) = - \cos(180-135) \\ \cos(135) = - \cos(45) \\ \cos(135) = - 0.5 \sqrt{2}

По теореме косинусов в ∆АВС:

{AC}^{2} = {AB}^{2} + {BC }^{2} - 2 \times AB \times BC \times \cos(ABC) \\ {AC}^{2} = {3}^{2} + {(2 \sqrt{2}) }^{2} - 2 \times 3 \times 2 \sqrt{2} \times \cos(135) \\ {AC}^{2} = 9 + 8 - 6 \times 2 \sqrt{2} \times ( - 0.5 \sqrt{2} ) \\ {AC}^{2} = 17 + 12

Совокупность:

АС=√29

АС=–√29

Так как длина задана положительным числом, то АС=√29.

ответ: √29


В треугольнике АВС АВ = 3 см, ВС =22 .Внешний угол при вершине В равен 45°. Найдите длину АС.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
S1nneR67 S1nneR67  17.09.2019 09:50
Визначте,яке з наведених тверджень є правильним,якщо трикутник abc ~ трикутнику klm. а) ав/вс=кm/lm б)ab/bc=kl/lm в)ab/bc=lm/mk г)ab/bc=kl/km...
vankovvandam vankovvandam  17.09.2019 09:50
Втреугольнике abc угол c = 90 градусов, sin a = 9 корней из 181 / корень из 181. найти: tg a. посмотрел уже кучу видеоуроков, так ничего и не понял....
Masha11781 Masha11781  17.09.2019 09:50
Найдите сторону bc треугольника abc, если ab = 6 дм, ac = 14 дм, угол b = 120градусов...
airflash1372 airflash1372  17.09.2019 09:50
Отрезки км и np пересекаются в точке о так, что kn=mp и kn// mp. докажите, что kp//mn, // - параллельно !...
3108200614041976 3108200614041976  10.07.2019 09:10
Решить ! ! в окружности проведены две перпендикулярные хорды ac и bd. найдите радиус окружности, если известно, что ab=3, cd=4....
arturka111 arturka111  10.07.2019 09:10
Центр окружности, описанной около треугольника abc лежит на стороне ab. радиус равен 10. найдите bc, если ac = 16...
Ketti08 Ketti08  10.07.2019 09:10
Как найти сторону равностороннего треугольника зная...
bati9999 bati9999  10.07.2019 09:00
Равнобедренные треугольники adc и bcd имеют общее основание dc. прямая ab пересекает отрезок cd в точке o. докажите что: а) угол adb равен углу acb; б) do равен oc. решите...
masha9form masha9form  10.07.2019 09:00
Стороны параллелограмма равны 44(см) и 88 (см), высота опущенная на 1 сторону равна 66(см). найдите высоту опущенную на 2 сторону....
Nastya080503 Nastya080503  10.07.2019 09:00
Отрезки ае и дс пересекаются в точке в,являющейся серединой каждого из них.1) докажите, что треугольникавс=треугольникуевд.2)найдите угол а и угол с треугольника авс,если...

Популярные вопросы