1. Геометрия
  2. В треугольнике ABC высота BH и

В треугольнике ABC высота BH и медиана СЕ пересекаются в точке O. Известно, расстояние что BO=4; OH=1; CE=5. Найдите сторону АВ. P.S. Решить без теореме Менелая и всяких готовых формул медиан.

1231231221312223 1231231221312223    2   21.07.2020 06:01    4

Ответы
PANDAnumber PANDAnumber  07.09.2020 01:22

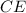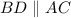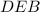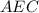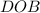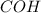Продлим CE до пересечения прямой BD\parallel AC. Треугольники DEB и AEC равны по стороне и двум прилежащим углам (т.к. СЕ - медиана, то AE = EB и ∠CEA = ∠DEB как вертикальные; ∠ACE = ∠BDE как накрест лежащие). Из подобия треугольников DOB и COH (по двум углам) следует пропорциональность соответствующих сторон.

\dfrac{BO}{OH}=\dfrac{BD}{CH}=\dfrac{DO}{CO}\Rightarrow~\dfrac{4}{1}=\dfrac{5-CO+5}{CO}\Rightarrow CO=2~ and~ AB=BD=4CH

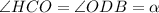Пусть \angle HCO=\angle ODB=\alpha, тогда по теореме косинусов :

OH^2=CH^2+CO^2-2CH\cdot CO\cos \alpha\\ OB^2=DO^2+BD^2-2DO\cdot BD\cos\alpha

1^2=CH^2+2^2-4CH\cos \alpha\\ 4^2=8^2+16CH^2-8\cdot 8CH\cos \alpha

От второго равенства отнимем первое, умноженное на 16

4^2-1^2=8^2-CH^2+16CH^2-2^2\\ \\ CH^2=3

CH=\sqrt{3}

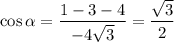Тогда \cos \alpha=\dfrac{1-3-4}{-4\sqrt{3}}=\dfrac{\sqrt{3}}{2}. По теореме косинусов для ΔDEB:

BE^2=BD^2+DE^2-2BD\cdot DE\cos \alpha=5^2+\big(4\sqrt{3}\big)^2-2\cdot 5\cdot 4\sqrt{3}\cdot \dfrac{\sqrt{3}}{2}=13

BE=\sqrt{13} отсюда AB=2BE=2\sqrt{13}.

ответ: 2√13


В треугольнике ABC высота BH и медиана СЕ пересекаются в точке O. Известно, расстояние что BO=4; OH=
ПОКАЗАТЬ ОТВЕТЫ
главный8 главный8  07.09.2020 01:22

2√13  без Менелая и всяких готовых формул медиан

Объяснение:


В треугольнике ABC высота BH и медиана СЕ пересекаются в точке O. Известно, расстояние что BO=4; OH=
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
AntihypeSPB AntihypeSPB  23.04.2020 15:53
Найди значения x и y при которых векторы -》а ( 21; x; 42) и -》(9; -6; y) будут коллинеарны ответ X = ? Y = ?...
Nikita20053103 Nikita20053103  23.04.2020 15:53
Чому дорівнює кут між бісектрисами двох вертикальних кутів?...
AльфаDog AльфаDog  23.04.2020 15:53
решить тест, записать нужно только варианты ответов, можно без пояснения...
DiANa24071 DiANa24071  23.04.2020 15:53
Перечертите рисунок 1, где треугольник ODB равносторонний. Проведите через точку В касательную. Найдите градусную меру угла между этой касательной и хордой BD ​...
popovArtem1156465156 popovArtem1156465156  23.04.2020 15:53
Решить 3 задачи по геометрии...
Angilass Angilass  23.04.2020 15:52
Нужно решить задачки по геометрии...
123фидан321 123фидан321  23.04.2020 15:52
Найдите радиус цистерны сферической формы для хранения газа, если её объём равен 113 1/3 м...
гугуляга гугуляга  23.04.2020 15:52
Найти градусную меру всех углов образованных при пересечении 2-х прямых, если один из них больше другого в 4 раза....
Patsanchik999 Patsanchik999  18.03.2019 07:50
Найдите площадь поверхности правильной четырехугольной призмы, если сторона её основания равна 10,а высота равна 6...
эмриханастчсия эмриханастчсия  18.03.2019 07:50
Один катет прямоугольного треугольника равен 3см. другой его катет а 1 см длиннее первого катета. гипотенуза треугольника на 2 см меньше суммы длин катетов. вычислите...

Популярные вопросы