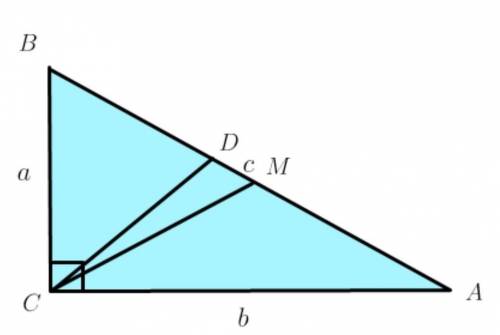
В треугольнике ABC угол C равен 90°. Угол между биссектрисой и медианой, проведёнными из вершины прямого угла, равен 8°. Вычисли меньший угол треугольника ABC. ответ дай в градусах.​

Для решения этой задачи нам понадобятся знания о свойствах биссектрис и медиан треугольника. 1. Биссектриса треугольника делит противоположную сторону на две отрезка, пропорциональных смежным сторонам треугольника. То есть, отношение длин сегментов биссектрицы и смежных сторон равно. 2. Медиана треугольника делит противоположную сторону пополам. Воспользуемся этими свойствами для решения задачи. Обозначим точки, где биссектриса и медиана пересекаются с противоположной стороной, как D и E соответственно. По свойству биссектрисы, отношение длины отрезка AD к длине отрезка DC равно отношению длины стороны AB к длине стороны BC: AD/DC = AB/BC По свойству медианы, отрезок DE делит сторону AC пополам: AE = EC Мы знаем, что угол между биссектрисой AD и медианой DE равен 8°. Обозначим этот угол как x. Поскольку угол ADE равен углу ADC, а угол DEC равен 90° (перпендикулярность медианы и прямого угла), то угол EDC равен 180° - x. Таким образом, мы можем записать следующие уравнения: 1) AD/DC = AB/BC 2) AE = EC 3) x + (180° - x) + 90° = 180° Теперь давайте решим систему уравнений последовательно: 1) Мы знаем, что AD/DC = AB/BC. Поэтому мы можем записать AB/BC = AD/DC. Заменим AB на AE + EB и BC на EC + CE, где EB и CE - это продолжения линий AD и CD соответственно. Теперь у нас имеется уравнение: (AE + EB)/(EC + CE) = AD/DC. 2)Мы знаем, что AE = EC. Поэтому мы можем заменить AE на EC и получим: (EC + EB)/(EC + CE) = AD/DC. 3) Теперь мы можем упростить уравнение, при этом мы знаем, что EC+CE это просто AC: (EC + EB)/AC = AD/DC. Мы знаем, что угол EDC равен 180° - x. Если мы подставим это соотношение, получим: (EC + EB)/AC = AD/DC = sin(180° - x). Теперь давайте рассмотрим третье уравнение: x + (180° - x) + 90° = 180°. Решим это уравнение: x + 90° = 180°. x = 180° - 90°. x = 90°. Окончательно, мы получили угол x равным 90°. Теперь вернемся к первому уравнению (EC + EB)/AC = AD/DC = sin(180° - x). Подставим значение угла x: (EC + EB)/AC = AD/DC = sin(180° - 90°). (EC + EB)/AC = AD/DC = sin(90°). (EC + EB)/AC = AD/DC = 1. Так как sin(90°) = 1, мы можем записать: (EC + EB)/AC = AD/DC = 1. Мы также знаем, что AE = EC, следовательно, AE/AC = 1. Умножим обе части уравнения на AC: AE = AC. Таким образом, мы получили, что в треугольнике АСE угол E равен 90°, то есть это прямой угол. Итак, меньший угол треугольника ABC равен углу E. Ответ: меньший угол ABC равен 90°.