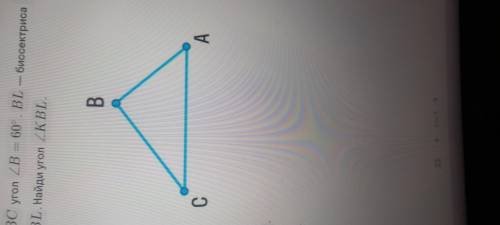
В треугольнике ABC угол B=60° . BL- биссектриса . А ВК - биссектриса АВL . Найди угол КВL

Для решения данной задачи, нам понадобится знание о свойствах биссектрисы и внутренних углах треугольника.

1. Вспомним свойство биссектрисы: она делит противолежащую ей сторону на отрезки, пропорциональные смежным сторонам треугольника. То есть, отношение отрезков, на которые биссектриса делит сторону, равно отношению смежных сторон треугольника. В данном случае, мы знаем, что BL - биссектриса треугольника ABC, поэтому AB/AL = BC/CL.

2. Последовательно применим свойство биссектрисы. По свойству биссектрисы BV и VC делят сторону BC пропорционально смежным сторонам треугольников – AC и AB, соответственно. Таким образом, получаем равенство BC/CL = AB/AK.

3. Сравнивая два полученных равенства, можем записать: AB/AL = BC/CL = BC/CK = AB/AK.

4. Зная, что два отношения равны, можно записать: AL = CK.

5. Из полученного равенства следует, что треугольники ALB и CKV равны по двум сторонам и углу между ними. Значит, угол КВL равен углу ЛВС (так как угол АЛВ и угол КВC – вертикальные и равны).

6. Поскольку угол B равен 60 градусам, угол ЛВС равен половине его, то есть 30 градусам.

Ответ: угол КВL равен 30 градусам.