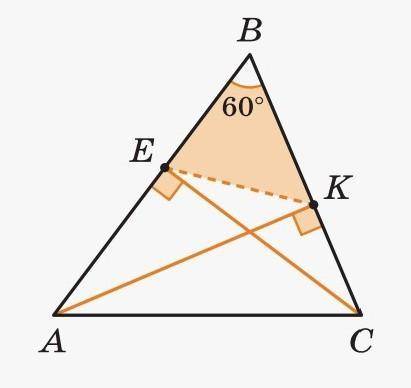
В  треугольнике ABC провели высоты AK и  CE. Найдите отношение,

в  котором отрезок EK делит площадь

треугольника, если угол ABC равен 60°​

Рассмотрим треугольник EKM:

Рассмотрим сторону KM:

Треугольник AKC:

это прямоугольный треугольник, угол AKC = 90°. KM - для данного треугольника - медиана, следовательно, KM = AM = MC.

Рассмотрим сторону EM:

Треугольник AEC:

это прямоугольный треугольник, угол AEC = 90°. EM - для данного треугольника - медиана, следовательно, EM = AM = MC.

Получается, KM = EM. Значит, треугольник MKE - равнобедренный................

Для решения данной задачи, мы можем воспользоваться свойствами высот треугольника и знаниями о площади треугольника.

Первым шагом определим площадь треугольника ABC. Мы знаем, что площадь треугольника можно найти, умножив половину произведения длин двух его сторон на синус угла между ними. В данном случае, у нас известна длина стороны BC, которая равна длине отрезка EK (обозначим ее как а), и угол ABC (равный 60°).

По формуле площади треугольника, имеем:

Площадь ABC = (1/2) * BC * CE * sin(ABC)

Подставим известные значения:

Площадь ABC = (1/2) * а * CE * sin(60°) ... (1)

Затем найдем площадь треугольников ABK и ACE, используя такую же формулу площади треугольника.

Площадь ABK = (1/2) * AB * AK * sin(ABK)
= (1/2) * а * AK * sin(60°) ... (2)

Площадь ACE = (1/2) * AC * CE * sin(ACE)
= (1/2) * а * CE * sin(60°) ... (3)

Так как высота треугольника разбивает его на два треугольника, отношение площади треугольника ABK к площади треугольника ACE равно отношению отрезка EK к отрезку KС.

Имеем:

Площадь ABK / Площадь ACE = ( (1/2) * а * AK * sin(60°) ) / ( (1/2) * а * CE * sin(60°) )
= (AK / CE)

Таким образом, отношение площади треугольника ABK к площади треугольника ACE равно отношению длины отрезка AK к длине отрезка CE.

Ответ: Отношение, в котором отрезок EK делит площадь треугольника, равно отношению длины отрезка AK к длине отрезка CE.