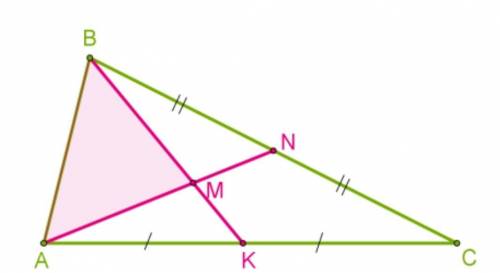
В треугольнике ABC проведённые медианы AN и BK пересекаются в точке М. Определи площадь треугольника АВС, если
площадь треугольника ABM равна 17 см².
ответ: SABC
см2.
Другие вопросы по теме Геометрия
Популярные вопросы
- Надо составить два уравнения. взаимодействие основных и кислотных...
1 - Вчем отличие творчества гайдна и моцатра?...
1 - Скажите радиус чтобы циркулем разделить отрезок 4см разделить на две...
1 - Вкаком порядке будешь искать слова в словаре ставить прятать украсить...
2 - Чему равен заряд, при переносе этого заряда в однородном электрическом...
1 - Решите пример столбиком 14484: 426...
3 - Запиши слова в три столбика. в1-й слова с ударением на первый слог....
1 - На рычаге уравновешены две гири массами 100г и 200г. определить длину...
2 - По небу плывёт пушистое облако.а вот ещё такое же белое и они медленно...
1 - Составьте 5 советов для младшего брата по поведению за столом использую...
1
Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Известно, что медианы треугольника пересекаются в одной точке, называемой точкой пересечения медиан.
Итак, у нас есть точка пересечения медиан М. Давайте обозначим точку пересечения медиан как М, а отрезки AM и BM как х и у соответственно.
Поскольку медиана делит сторону на две равные части, можно сделать вывод, что отрезок AM равен отрезку MB.
Давайте теперь рассмотрим треугольник ABM. По условию задачи, мы знаем, что его площадь равна 17 квадратных сантиметров.
Мы можем использовать свойство медианы, чтобы найти площадь треугольника ABC.
Так как AM и MB равны, то он делит площадь треугольника ABC на две равные части.
Поэтому площадь треугольника ABC равна удвоенной площади треугольника ABM.
То есть, S(ABC) = 2 * S(ABM).
Подставим известное значение площади треугольника ABM в формулу:
S(ABC) = 2 * 17 = 34 квадратных сантиметра.
Таким образом, площадь треугольника ABC равна 34 квадратных сантиметра.