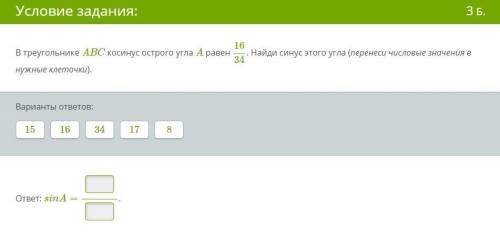
В треугольнике ABC косинус острого угла A равен 16/34. Найди синус этого угла

Для решения этой задачи, нам понадобятся соотношения между косинусом и синусом острого угла в прямоугольном треугольнике.

Вспомним, что косинус острого угла A в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. То есть в нашем случае, это отношение будет равно 16/34.

По теореме Пифагора, в прямоугольном треугольнике длина гипотенузы (BC) в квадрате равна сумме квадратов длин катетов (AC и AB):
BC² = AC² + AB²

Используя наши обозначения, получаем:
BC² = (16)² + (34)²
BC² = 256 + 1156
BC² = 1412

После вычислений мы получили значение BC² равное 1412.

Теперь, чтобы найти длину BC, нужно извлечь квадратный корень из 1412:
BC = √1412
BC ≈ 37.6

Затем, чтобы найти синус острого угла A, мы используем соотношение между синусом и гипотенузой в прямоугольном треугольнике. Синус острого угла A в нашем случае будет равен отношению противолежащего катета к гипотенузе, то есть отношению AB к BC:
синус A = AB/BC

Подставляя значения AB и BC, получаем:
синус A = 34/37.6
синус A ≈ 0.9043

Итак, синус острого угла A в треугольнике ABC примерно равен 0.9043.