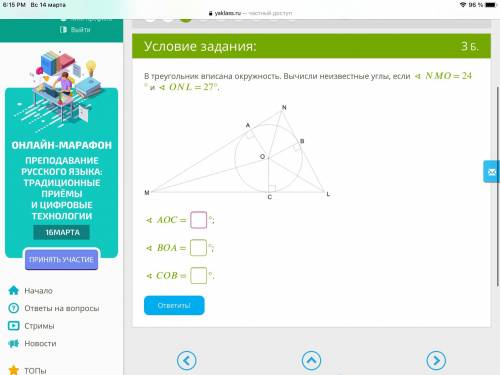
В треугольник вписана окружность.вычисли неизвестные углы,если угол NMO=24 и угол ONL=27

Добрый день! Давайте вместе решим эту задачу.

Дано, что треугольник ABC вписан в окружность, где точка O - центр окружности.

У нас есть следующая информация об углах:
Угол NMO = 24 градуса (если N - вершина треугольника и NM - касательная к окружности, то угол NMO является половиной угла между касательной и хордой).
Угол ONL = 27 градусов (если O - центр окружности, а ON - радиус и NL - касательная, то угол ONL является половиной угла между радиусом и хордой).

Нам нужно определить неизвестные углы треугольника ABC. Для этого мы можем воспользоваться свойствами вписанного угла и свойством суммы углов треугольника.

Свойство вписанного угла: Если угол лежит на дуге, то его мера равна половине меры дуги.
Свойство суммы углов треугольника: Сумма углов треугольника равна 180 градусов.

Давайте обозначим неизвестные углы треугольника ABC следующим образом:
Угол ABC = x градусов
Угол BCA = y градусов

Теперь мы можем записать уравнения, используя свойства треугольника:
x + y + 90 = 180 (сумма углов треугольника равна 180 градусов)
x + y = 90

Также мы можем использовать свойства вписанного угла:
x = 2 * y (угол ABC равен двум углам BCA, так как угол ABC лежит на дуге BCA и каждый угол лежит на половине дуги)

Теперь у нас есть система уравнений:
x + y = 90
x = 2 * y

Решим эту систему уравнений методом подстановки.
Подставим второе уравнение в первое:
2 * y + y = 90
3 * y = 90
y = 30

Теперь найдем значение x, подставив y = 30 во второе уравнение:
x = 2 * 30
x = 60

Итак, угол ABC равен 60 градусов, а угол BCA равен 30 градусов.

Надеюсь, что мой ответ был понятен для вас! Если у вас остались какие-либо вопросы, пожалуйста, не стесняйтесь задавать их. Я буду рад помочь!