В трапецию ABCD с основаниями BC и AD вписана окруж- ность с центром в точке 0. Площадь треугольника АОВ отно-
сится к площади треугольника COD как 1:3. Тогда отношение
sin A: sinD равно... .​

В трапецию ABCD с основаниями BC и AD вписана окружность с центром в точке 0. Площадь Δ АОВ относится к площади Δ COD как 1:3. Тогда отношение  sin A: sinD равно... .​

Объяснение:

Центр вписанной окружности O лежит в точке пересечения биссектрис углов трапеции. Соединим т. О с точкой касания окружности с боковыми сторонами . Это будет радиус и высота ΔАОВ и ΔCOD ( кстати, прямоугольных) .

S(AOB)=0,5*AB*r   ,S(COD)=0,5*CD*r  . Тогда отношение

.

Пусть ВК⊥АD ,СР⊥АD.  BK=CP =h

ΔABK-прямоугольный ,sin A= .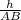

ΔDCP-прямоугольный ,sin D= .

Отношение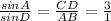      .