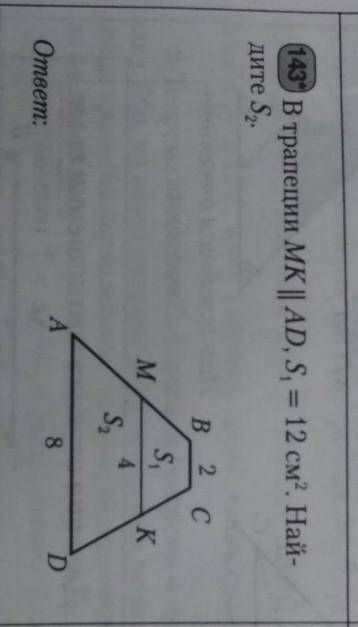
В трапеции MK||AD, S1=12см2. Найдите S2

Для решения данной задачи, нам необходимо использовать свойства трапеции.

1. Данный вопрос говорит о том, что трапеция MK||AD. Это значит, что линия MK и AD параллельны друг другу.

2. В трапеции MK||AD, мы также знаем, что площадь S1 составляет 12 см².

Для нахождения второй площади S2, мы должны использовать свойство трапеции: отношение площадей двух трапеций, имеющих одинаковую высоту и основания.

Основаниями трапеции являются отрезки AD и MK. То есть, S1 и S2 будут иметь одну и ту же высоту и одно из оснований.

3. Представим, что мы можем разделить трапецию на две части, таким образом, чтобы S1 и S2 образовали две маленькие трапеции. Для этого построим прямую, параллельную основаниям трапеции MK и AD, и проходящую через точку S1.

4. Теперь мы можем видеть, что S1 и S2 образуют две маленькие трапеции. Обозначим их площади как S1_1 и S1_2 соответственно.

5. Очевидно, что S1_1 и S1_2 имеют одно основание (обозначим его как х) и одну высоту. Таким образом, отношение S1_1 к S1_2 равно отношению их оснований.

6. Теперь нам нужно найти отношение оснований трапеций S1 и S2 (то есть отношение х к АД).

7. Используя свойство параллельных линий и подобных треугольников, мы можем заключить, что отношение MK к АД равно отношению S1 к S2.

8. Так как MK равен 5 см, значит отношение MK к АД равно 5/12.

9. Мы можем записать равенство: 5/12 = S1/S2.

10. Теперь, чтобы найти S2, нужно решить уравнение относительно S2: S2 = (12 * 5) / 12 = 5 см².

Таким образом, площадь S2 равна 5 см².