В тетраэдре SABCSABC точками обозначены середины рёбер. Определи, перпендикулярны ли эти пары прямых. выбери верные варианты ответа из списка.
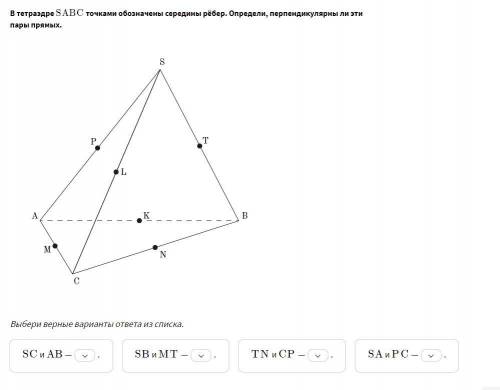
Ответы
Чтобы определить, перпендикулярны ли эти пары прямых, мы можем воспользоваться знакомыми правилами о перпендикулярности. Для этого, нам необходимо проверить, что произведение коэффициентов наклона каждой пары прямых равно -1.
1) Найдем коэффициенты наклона прямых SA и SC.
Прямая SA проходит через точки S(-1, 2, 0) и A(1, -2, -2).
Коэффициент наклона можно найти по формуле: m = (y2 - y1) / (x2 - x1)
m_SA = (-2 - 2) / (1 - (-1)) = (-4) / 2 = -2
Прямая SC проходит через точки S(-1, 2, 0) и C(1, 0, 4).
m_SC = (0 - 2) / (1 - (-1)) = (-2) / 2 = -1
2) Найдем коэффициенты наклона прямых SB и SA.
Прямая SB проходит через точки S(-1, 2, 0) и B(-1, -2, 2).
m_SB = (-2 - 2) / (-1 - (-1)) = (-4) / 0 = undefined
Прямая SA проходит через точки S(-1, 2, 0) и A(1, -2, -2).
m_SA = (-2 - 2) / (1 - (-1)) = (-4) / 2 = - 2
3) Найдем коэффициенты наклона прямых SB и SC.
Прямая SB проходит через точки S(-1, 2, 0) и B(-1, -2, 2).
m_SB = (-2 - 2) / (-1 - (-1)) = (-4) / 0 = undefined
Прямая SC проходит через точки S(-1, 2, 0) и C(1, 0, 4).
m_SC = (0 - 2) / (1 - (-1)) = (-2) / 2 = -1
Теперь, проверим, выполняется ли условие произведения коэффициентов наклона.
1) m_SA * m_SC = (-2) * (-1) = 2
Так как произведение равно 2, эти прямые не являются перпендикулярными.
2) m_SB * m_SA = undefined * (-2) = undefined
Так как произведение равно undefined, мы не можем сделать вывод о перпендикулярности.
3) m_SB * m_SC = undefined * (-1) = undefined
Так как произведение равно undefined, мы не можем сделать вывод о перпендикулярности.
Таким образом, из всех пар прямых только прямые SA и SC не являются перпендикулярными, тогда как для прямых SB и SA, и SB и SC мы не можем сказать, перпендикулярны они или нет, потому что их коэффициенты наклона неопределены.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- *9*-5*2=246тут тоже надо вставить числа в вместо звёздочек...
2 - Состав и структура сообщества 1.Морфологическая структура сообщества-это...
1 - Більша діагональ і сторона ромба відповідно дорівнює 4 корінь 14 см і...
3 - ответить на во Герой нашего времени ) 1.Какое дело было у Печорина и...
1 - AlCl3 + NaOH(избыток)=NaAl(OH)4+HCl(недостаток буду благодарен ! Заранее...
1 - 1) Какова главная тема творчества Абрамова? О чём были его произведения?...
1 - Даны координаты точки. Определи, в какой координатной четверти находится...
1 - Твір на тему Добро завжди перемагає зло 5 клас...
1 - да я знаю это легко, ноя. пропустила эту тему и болела( Зарание...
2 - План Пригоди Тома Сойєра ...
2