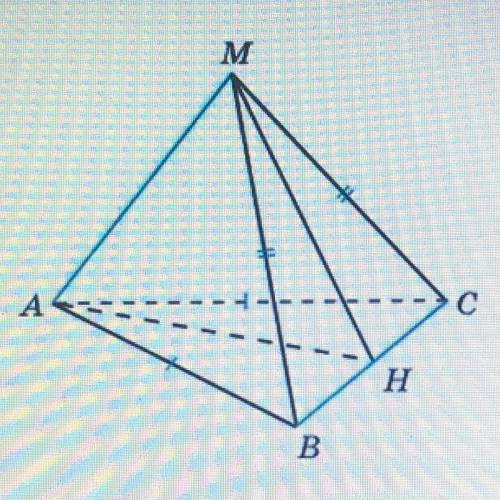
В тетраэдре МАВС АВ=АС, МВ=МС. Докажи, что ВС_|_(перпендикулярна)АМ.

Добрый день! Рада буду помочь вам с вашим вопросом.

Для доказательства, что отрезок ВС перпендикулярен отрезку АМ, нам необходимо провести несколько логических шагов. Опираясь на некоторые известные факты о тетраэдрах, мы можем прийти к нужному заключению.

Шаг 1: Вспомним основные определения и свойства тетраэдра. Тетраэдр - это многогранник, состоящий из четырех треугольных граней. Каждая грань тетраэдра представляет собой треугольник.

Шаг 2: Обратимся к данному в условии равенству отрезков: АВ = АС и МВ = МС. Это означает, что стороны АВ и АС равны между собой, а стороны МВ и МС также равны.

Шаг 3: Воспользуемся следующим свойством: в треугольнике, где две стороны равны, соответствующие им углы также равны. Это называется свойством равенства треугольников по стороне и двум углам.

Шаг 4: Поскольку стороны АВ и АС равны, связанные с ними углы МАВ и МАС также равны. Аналогично, угол МВА равен углу МСА.

Шаг 5: Заметим, что угол МВА и угол МАС являются вертикальными углами, поскольку они образованы пересечением прямых МВ и МАС, и прямых МА и МВА. Вертикальные углы равны между собой.

Шаг 6: Из шага 4 следует, что угол МВА равен углу МСА. Из шага 5 следует, что угол МВА равен углу МАС. Таким образом, углы МСА и МАС равны между собой.

Шаг 7: Из шага 6 следует, что треугольник МСА является равносторонним треугольником.

Шаг 8: Так как треугольник МСА является равносторонним, все его высоты, включая высоту, проведенную из вершины С, перпендикулярны основанию. Основание треугольника МСА - это отрезок АМ. Таким образом, отрезок ВС перпендикулярен отрезку АМ.

Таким образом, мы доказали, что ВС перпендикулярна АМ на основании данных и логических выводов, представленных выше.