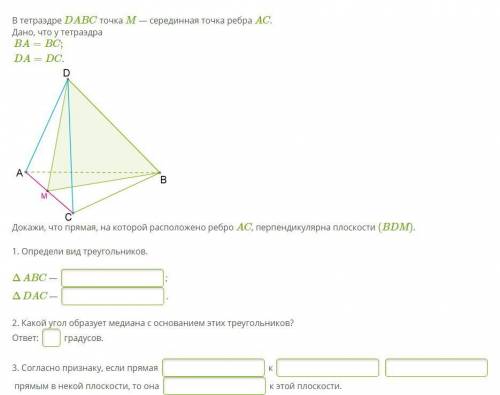
В тетраэдре DABC точка M — серединная точка ребра AC. Дано, что у тетраэдра
BA=BC;DA=DC.
Докажи, что прямая, на которой расположено ребро AC, перпендикулярна плоскости (BDM).
1. Определи вид треугольников.
ΔABC —
ΔDAC —
2. Какой угол образует медиана с основанием этих треугольников?
ответ: градусов.
Другие вопросы по теме Геометрия
Популярные вопросы
- найдите боковую сторону равнобедренного треугольника если его основание...
3 - В мензурку налита вода, высота столба которой h= 40 см. Найдите давление...
3 - (2а-5)2+(3а-5)(5+3а)+30а при а ❗️❗️❗️...
2 - Один из внешних углов прямоугольного треугольника равен 140°. Найди острые...
1 - Какие условия могут быть причиной огнеопасных ситуаций? Подготовить информацию!...
2 - Безусловный рефлекс * звонок будильника по утрамобезвоживание при недостатке...
1 - 8. Приведите примеры механической энергии в мире живой природы ( не менее...
2 - Если можете дайте все ответы...
3 - Литам-ган.Обладателем каких талантов являлся А...
3 - AB=25cm BC=20cнайти cos B?tgA?...
2
Первым шагом мы должны определить вид треугольников ΔABC и ΔDAC. У нас уже дано, что в тетраэдре DABC точка M является серединной точкой ребра AC. Из этого следует, что отрезок BM делит ребро AC пополам.
Так как у тетраэдра BA=BC и DA=DC, то стороны AC и BD будут иметь одинаковую длину. Таким образом, треугольники ΔABC и ΔDAC будут равнобедренными, так как у них две равные стороны - BC и AC.
Теперь перейдем к следующему вопросу - какой угол образует медиана с основанием этих треугольников?
У нас есть два треугольника, ΔABC и ΔDAC, и оба они равнобедренные. Значит, угол между основанием и медианой каждого из этих треугольников будет равным углу, образованному биссектрисой этого треугольника и боковой стороной.
Мы можем обозначить углы каждого из треугольников следующим образом: угол ABC = α, угол BAC = β и угол B = γ. Тогда у нас будет угол AMB = γ, так как BM делит ребро AC пополам и AMB - прямой угол.
Используя свойство равнобедренных треугольников, мы можем сказать, что угол BAD = угол B = γ, а угол ABD = угол ABC = α.
Теперь, чтобы доказать, что прямая, на которой расположено ребро AC, перпендикулярна плоскости (BDM), нам нужно показать, что угол AMB и угол BAD равны. Как уже установлено, угол AMB = γ, и мы видим, что угол BAD тоже равен γ, поскольку оба угла α и γ получаются при делении прямого угла.
Таким образом, мы доказали, что угол AMB равен углу BAD. А два угла, равных друг другу, являются вертикальными углами, а значит, прямая, на которой расположено ребро AC, перпендикулярна плоскости (BDM).
Надеюсь, что мое объяснение было понятным и помогло вам понять решение задачи. Если у вас возникнут еще вопросы, не стесняйтесь задавать их.