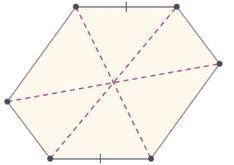
В шестиугольнике две противоположные стороны параллельны и равны, а другие пары противоположных сторон параллельны. Докажите, что три его диагонали, соединяющие противоположные вершины, пересекаются в одной точке с объяснением)
Другие вопросы по теме Геометрия
Популярные вопросы
- Цена некоторого товара снизилась со 180 до 126 На сколько процентов снизилась...
1 - Написать эссе на тему Хранители культурно-исторических традиции, народные ремесла...
3 - . К какому стилю речи относится приведенный ниже текст? Остались мы одни в...
3 - Джамбул Жабаев Зілді приказ . Урок 2 ИЛИ 20...
3 - даю 20 мин чтобы это все решили...
3 - Скажи зачем тебе и лучший ответ...
2 - Разберите эти слова по составу :невдалеке,неподалёку,невмоготу,невпопад,недаром,...
3 - Почему любая система образования в нашем современном обществе обязательно предполагает...
2 - Ауаны қасиеттеріне байланысты адамның тіршілігінде қолдануға мысал тауып орналастыр...
1 - В результате весеннего наводнения жителям деревни был причинен ущерб: затоплено...
1
Для доказательства того, что три диагонали шестиугольника, соединяющие противоположные вершины, пересекаются в одной точке, мы воспользуемся свойством параллелограмма.
Шестиугольник, в данном случае, является параллелограммом. Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны. В данном шестиугольнике имеем, что две противоположные стороны (AD и CF) параллельны и равны, а также другие пары противоположных сторон (AB и DE, BC и EF) также параллельны.
Итак, пусть AC и BD - две диагонали, соединяющие противоположные вершины шестиугольника. Чтобы доказать, что диагонали пересекаются в одной точке, мы воспользуемся свойством параллелограмма, что диагонали параллелограмма делятся пополам.
Проведем диагональ CE. По условию, мы знаем, что сторона BC параллельна и равна стороне EF, следовательно, угол BCE равен углу CEF (так как смежные углы при параллельных прямых равны). Также, угол BCD равен углу FCE (также по свойству параллельностей).
Мы имеем два равных угла в треугольниках BCD и FCE, и одна сторона (BC) равная стороне EF. По теореме об угле-прилежащем у равных сторон получаем, что треугольники BCD и FCE равны по двум углам и одной стороне.
Теперь мы знаем, что эти два треугольника равны. Следовательно, диагональ CE делит диагональ AC пополам. Аналогично, проведенная диагональ CE делит диагональ BD пополам.
Теперь, поскольку диагонали AC и BD делятся диагональю CE пополам, мы можем заключить, что все три диагонали пересекаются в одной точке, которой является точка E.
Таким образом, мы доказали, что три диагонали шестиугольника пересекаются в одной точке.
Я надеюсь, что объяснение было понятным и полным. Если у вас есть еще вопросы, не стесняйтесь задавать.