В равностороннем треугольнике ABC со стороной 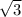 проведены три биссектрисы AN, BH и CM. Найдите периметр треугольника ALH.
проведены три биссектрисы AN, BH и CM. Найдите периметр треугольника ALH.
Другие вопросы по теме Геометрия
Популярные вопросы
- На 3 грузовиках привезли 180 мешков муки сколько потребуется грузовиков...
1 - З двох міст, відстань між якими 600 км, одночасно назустріч один...
3 - Привет, ИТАК ХАЛЯВНЫЕ Что было между Бурундук и Касым ханами?...
2 - Составить схему образования химической связи ЧТОБ БЫЛО ПОНЯТНО...
2 - Постройте график : 1) х+2у=8 2) 3х = -6 3) 5у = 10...
2 - Найти величину угла на рисунке ...
1 - речення (0.5б) А.Остап сів у човен, і Соломія одіпхнулась од берега...
1 - 1. Однорідні члени речення — це: A. члени речення, що становлять...
3 - Из одной точки к окружности проведены две касательные. Отрезок...
2 - Христиане объединяется в ассоциации общины картели Куда именно...
2
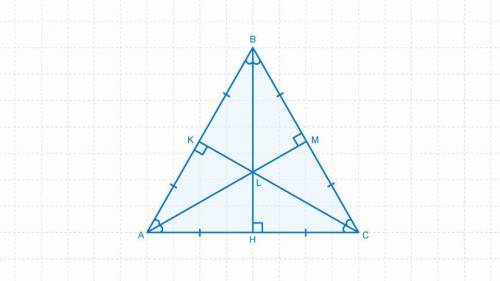
В равностороннем треугольнике АВС со стороной, равной √3, проведены три биссектрисы : AM, BH, CK. Найдите периметр треугольника ALH.
- - -
Дано :
ΔАВС - правильный (равносторонний).
АВ = √3.
АМ, ВН, СК - биссектрисы.
АМ ∩ ВН ∩ СК = L.
Найти :
Р(ΔALH) = ?
АВ = ВС = АС = √3 (по определению равностороннего треугольника).
В правильном треугольнике все его биссектрисы являются медианами и высотами.Соответственно, по определению медианы треугольника -
АН = НС =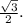
Рассмотрим ΔALH - прямоугольный (так как ∠AHL= 90° по определению высоты).
В равностороннем треугольнике все углы равны по 60°.То есть ∠А = 60°.
По определению биссектрисы треугольника -
∠ВАМ = ∠МАС = 60°/2 = 30°.
По определению косинуса острого угла прямоугольного треугольника -
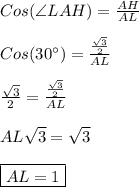
В прямоугольном треугольнике против угла в 30° лежит катет, равный половине гипотенузе.Отсюда -
LH = 0,5*AL = 1*0,5 = 0,5.
Периметр - это сумма длин всех сторон.Отсюда -
Р(ΔALH) = LH + AL + AH =