В равнобедренный треугольник ABC с основанием AC вписана окружность. Она касается стороны BC в точке P. Отрезок AP пересекает окружность точке D. Найдите площадь треугольника ABC, если известно, что AC = 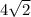
, DP = 2.
Другие вопросы по теме Геометрия
Популярные вопросы
- Какое максимальное знач.принимает число Р,если оно не делиться на 12?...
2 - при взаимодействии 6 литров азота с избытком водорода образовался аммиак...
3 - у каких из перечисленных насекомых происходит развитие с полным превращениему...
2 - Та 1. Nariлi окып, екі палы аурумен байланыстар... Mini и максатта лекарсытылы...
2 - Используя рисунок, выполните задание я...
3 - ХИМИЯ 8 КЛАСС 1. Изобразите кристаллическую решетку: а) иода, алмаза, хлорида...
2 - Эссе на английском. Должно быть 80 слов 1)When will your next holiday be?2)Which...
3 - Что стало главным источником дохода ост-индской компании после завершения...
2 - Придумайте и запишите три предложения с СКС, используя одну из степеней...
3 - 1. Прочитайте отрывок из поэмы Н. В. Гоголя «Мертвые души». Определите его...
3
По теореме о секущей и касательной:
По теореме Виета, получим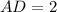 .
.
Рассмотрим треугольник APC со сторонами AP = 4; PC =2√2 и AC = 4√2 и пусть ∠C = α. Используем теорему косинусов:
cos α = (a² + b² - c²)/2ab = ((4√2)² + (2√2)² - 4²)/[2*4√2*2√2] = 3/4
Из определения косинуса cos a = CK / BC отсюда BC = CK/cosa тогда получим BC = 2√2 / [3/4] = 8√2/3
По теореме Пифагора:
Искомая площадь треугольника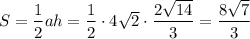 кв. ед.
кв. ед.