в равнобедренной трапеции диагональ перпендикулярна боковой стороне. найти площадь трапеции если большее основание равно 12 √ 3 , а один из углов трапеции равен 60° . ВСЁ РАСПИСОВАТЬ.
Другие вопросы по теме Геометрия
Популярные вопросы
- Составить план по любой сказке (моя любимая сказка колобок...
3 - Зведи до найменшого спільного знаменника дроби: 2/3,3/4 і 7/12; 2/3, 1/9 і 7/18;...
1 - Объяснить два афоризма о языке 1)что язык — один из богатейших языков в мире, в...
2 - Never/to the beach/in winter/go/we составьте предложение!...
2 - Докажи что у первобытных людей зародилось искусство...
1 - Спрости вираз 1) 8*7*x 2) 17x*2 3) 5*x*9*t 4) 9a*11b 5) 5*x*9*8*a*t 6) 10b*20c*17p...
3 - Перечисли биологические признаки, которые наследует человек?...
1 - Вбочке 20 литров воды,а в цистерне в 5 раз больше. сколько всего литров воды в...
1 - Найдиие значение выражения (38×201+4242: 21)-7829...
3 - Можете перевести 1)you won t go with me next time. 2)i won t speak to him. 3)it...
3
ответ:SABCD=81√3см²
Объяснение:
SABCD=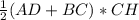
1.ΔADB(∠B=90°):
∠ADB=90-∠BAD=90-60=30°(Сумма острых углов прямоугольного треугольника равна 90)
AB=1/2AD=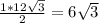 см(Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.)
см(Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.)
2.Трапеция ABCD:
AB=CD=6√3см(В равнобокой трапеции боковые стороны равны)
∠A=∠D=60(В равнобокой трапеции углы при основаниях равны)
3.ΔDCH(∠H=90°):
∠DCH=90-∠CDH=90-60=30°(Сумма острых углов прямоугольного треугольника равна 90)
HD=1/2CD=6√3/2=3√3см(Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.)
sinCDH=CH/CD
CH=sinCDH*CD=sin60*6√3=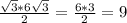 см
см
4.Трапеция ABCD:
AD-BC=2HD
-BC=-AD+2HD
BC=AD-2HD=12√3-2*3√3=12√3-6√3=6√3см
SABCD=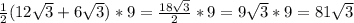 см²
см²