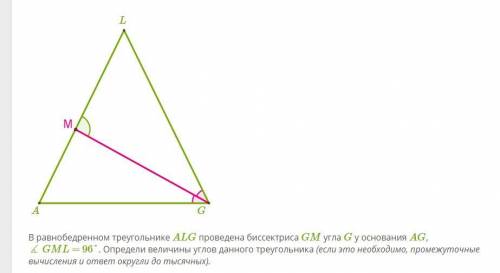
В равнобедренном треугольнике ALG проведена биссектриса GM угла G у основания AG, ∡ GML = 96°. Определи величины углов данного треугольника (если это необходимо, промежуточные вычисления и ответ округли до тысячных).
Другие вопросы по теме Геометрия
Популярные вопросы
- Подберите к словам синонимы (если можно подобрать) куть,середа,коник....
1 - Крутизной лестницы называют отношение высоты ступеньки к ее глубине...
2 - 63,75 г оксида алюминия , содержащего 20% примесей , обработали избытком...
2 - Рабочии заасфольтировали дорого за 12 дней.какую часть дороги заасфальтировали...
2 - 2. какой объем хлора(н.у) потребуется для вытеснения йода из 450 г...
1 - Подбери синоним к слову удивительный...
3 - Что такое формализация? можно ли назвать выставленные оценки учителем...
1 - Составить отрицательные предложения: 1. i (do) 2. we (have) 3. they...
1 - у какого элемента больше выражены неметаллические свойства у серы или...
2 - Механическая и переработка пищи называется пищеварение выделение дыхание...
1
Биссектриса MG — делит угол G пополам.
Объявим <A & <MGA — как переменные: <A = 2x; <MGA = x.
<AMG = 180-96 = 84°.
Сумма углов треугольника равна 180°, тоесть, уравнение таково:
Вывод: <L = 52°; <A == <G = 64°.
ответ:∠L=52°, ∠A=64°, ∠G=64°
Так как треугольник равнобедренный с основанием AG, то углы при основании равны
∠A=∠G =х
А ∠ GML - внешний угол Δ AМG
∠ GML =∠А+1/2∠ G;
х+1/2 х=96°;
х=96° : 3/2;
х=64°- величина углов∠Aи∠G
По теореме о сумме трёх углов треугольника :
∠L=180°-2∠A=180°-2*64°=52°