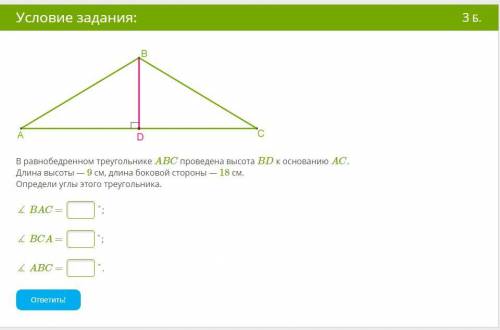
В равнобедренном треугольнике ABC проведена высота BD к основанию AC. Длина высоты — 9 см, длина боковой стороны — 18 см.
Определи углы этого треугольника.
Другие вопросы по теме Геометрия
Популярные вопросы
- Сочинение на тему как я покупал собаку...
1 - Площадь поверхности земли равна 506 целых 2/3 млн. км.кв. , а луны 38 млн....
2 - Длина отрезка ab равна 40 см точки c и d делят отрезок ab на отрезки ac...
1 - Поставить ударение.указать имя собственное. звери ванюшу так лаского любят,звери...
3 - Где деепричастные обороты? : старый, обширный, тянувшийся позади дома сад,...
1 - Как назывался свод бытовых правил при иване грозном...
2 - Вкаком предложении придаточную часть сложноподчиненного предложения нельзя...
1 - Как найти сумму всех целых чисел, больших -7, но меньших 6 заранее...
1 - Болото,реки,озера,ледники значения для человека и природы.кратко...
2 - Укажите грамматически правильное продолжение предложения. войдя в переполненный...
3
BAC 30°
BCA 30°
ABC 120°
Объяснение:
По свойству равнобедренного треугольника, высота, проведенная к основанию, является также медианой и биссектрисой. Это означает, что угол ABD является прямым, а угол DBC является углом при основании и равен половине верхнего основания, т.е. угол DBC = (180° - угол ABC) / 2.
Мы знаем, что длина высоты BD равна 9 см и длина боковой стороны AB равна 18 см. Чтобы найти угол ABC, мы можем использовать тригонометрию.
Обозначим угол ABC как x. Затем мы можем использовать тригонометрическую функцию синуса, чтобы найти значение угла ABC.
sin(x) = противолежащая сторона / гипотенуза
sin(x) = BD / AB
sin(x) = 9 / 18
sin(x) = 1 / 2
Поскольку sin(x) = 1 / 2, мы должны найти угол, значение синуса которого равно 1 / 2. Из таблицы значений синуса мы видим, что угол, значение синуса которого равно 1 / 2, равен 30°.
Таким образом, угол ABC равен 30°.
Теперь мы можем найти угол DBC, используя формулу, указанную ранее:
угол DBC = (180° - угол ABC) / 2
угол DBC = (180° - 30°) / 2
угол DBC = 150° / 2
угол DBC = 75°
Итак, углы треугольника ABC равны 30°, 75° и 75°.