1. Геометрия
  2. в равнобедренном прямоугольном

в равнобедренном прямоугольном треугольнике abc с прямым углом c гипотенуза равна 8 найти а) катет ас б) высоту CD проведённую к гипотенузе

nastyarybinskap0ai9q nastyarybinskap0ai9q    3   03.03.2020 10:51    1

Ответы
Alesja4788 Alesja4788  11.09.2020 20:12

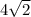а)4\sqrt{2} б) 4

Объяснение:

По формуле гипотенузы вычислим катеты, т.к. треугольник равнобедренный, то

c=\sqrt{2a^{2} }\\ 8=a\sqrt{2}\\ a=\frac{8}{\sqrt{2} }\\ a=\sqrt{\frac{64}{2} }\\ a=\sqrt{32}=4\sqrt{2} \\

б)

Высота в равнобедренном треугольнике является и медианой и биссектрисой угла. Следовательно угол DCB = 90/2=45 градусов.

Треугольник ABC-равнобедренный, значит угол А=В=45 градусов.

Из этого следует, что треугольник DCB-равнобедренный и высота CD равна половине гипотенузы треугольника ABC, CD=8/2=4

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
саша3421342 саша3421342  04.06.2019 08:50
1.сторона ромба равна ,острый угол равен 60 градусов.найдите радиус вписанной окружности. 2.около трапеции описан окр. р=96, средняя линия равна 16.найдите боковую сторону...
y6yyy y6yyy  04.06.2019 08:50
Дано: а,в,с лежат на одной прямой ав = 10.8 см, вс = 2,4 см. найти ас...
olka52 olka52  21.05.2020 07:35
Памагите с любым заданием у меня соч...
f0xses f0xses  21.05.2020 07:35
5. Постройте треугольник по 2 сторонам и углу между ними (пошагово записывая построение) AB=3см А В ВС=4см ВС и ∠АВС=30 о ....
innapuna8 innapuna8  21.05.2020 09:05
4. а) Изобразите окружность, соответствующую уравнению (x −5)2 + (y −10)2 =25 b) Определите взаимное расположение прямой y = 5 и окружности (x −5)во второй степени + (y −10)...
Diana17273839 Diana17273839  22.05.2020 09:26
В треугольнике ABC стороны AB = 6, BC = 3, AC = 5. На стороне AC взята точка M так, что AM/МС=3/2. Найдите BM....
nikanor020499 nikanor020499  21.05.2020 07:35
3 Реши задачи. К каждой задаче построй чертёж (рисунок). А)Найдите неизвестный угол треугольника, если два других угла равны: 25 градусов и 120 градусов . В)Найдите углы равнобедренного...
Ivan733822 Ivan733822  21.10.2020 12:53
Пряму задано рівнянням 4x+3y=0 1) Знайдіть координати точок перетину прямої з осями координат.2) Знайдіть периметр трикутника, обмеженого осями координат і прямою.​...
Vika3839 Vika3839  21.10.2020 12:53
Построить три вида детали по аксонометрической проекции....
polina030502 polina030502  02.07.2019 04:30
Как найти площадь трапеции если её основания равны 10 и 20 а боковые стороны 6 и 8...

Популярные вопросы