В прямоугольной трапеции основания равны 5 и 7,4. Меньшая диагональ есть биссектрисой тупого угла. Вычислить периметр трапеции

26.8

Объяснение:

Выполним рисунок. (см. Рис. 1)

Прямоугольная трапеция ABCD, меньшее основание BC=5, большее основание DA=7.4,  AC -биссектриса ∠С, AB⊥BC, AB⊥DA, DA║BC.

∠ACD=∠ВСА т.к. АС- биссектриса,

∠DAC=∠ВСА, как накрест лежащие, значит  ∠ACD=∠DAC=∠ВСА.

ΔACD-равнобедренный, т.к. ∠ACD=∠DAC. Тогда AD=CD=7.4.

Выполним дополнительное построение (см. Рис. 2). Проведем высоту DO в ΔACD. Т.к. ΔACD-равнобедренный, то DO также является медианой, значит, AO=OC.

Пусть АО=х, тогда АС=2х.

ΔАВС ~ ΔDAO по двум углам ∠DAC=∠ВСА и ∠АВС=∠AOD=90°.

Тогда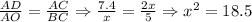

Из прямоугольного ΔАВС найдем катет АВ:

.

Значит в трапеции ABCD: AB=7, BC=5, CD=7.4, DA=7.4.