В прямоугольном треугольнике ОВF угол = 90°, ОК - перпендикуляр к FB, BF = 24см, ВК =18 см. Найдите ОК, ОB, sin yгла ОВF
Другие вопросы по теме Геометрия
Популярные вопросы
- Розвязати систему рівнянь підстановок 3х+4y=0 x-2y=11...
3 - Соя содержит 40% белка, 29% крахмала и 20% жиров. сколько крахмала...
1 - Запишіть спільнокореневі слова- птах, козак, учень, юнак, комаха,...
1 - Написати 3 ( не коротких) речення і позначити частини мови іново...
2 - Образуйте из существительных женского рода, существительные мужского...
3 - Спешите. красной кистью рябина зажглась. подчеркните в придложении...
3 - Сушествует ли крёстный брат или сестра?...
2 - Катер плыл 2 ч. со скоростью 35 км/ч.. потом он увеличел скорость...
3 - Слово қыдыру в 3 временах просклонять...
1 - Iam a pupil составить вопрос к предложению...
3
OK=6 , OB=12
, OB=12 , sin∠OBF=
, sin∠OBF=
Объяснение:
OK= =
=  =
=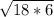 =
= =6
=6
OB=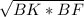 =
=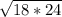 =
=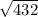 =12
=12
по теореме Пифагора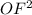 =
= -
-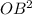 =
=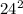 -
- =576-432=144
=576-432=144
OF=12
sin ∠OBF=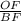 =
= =
=