В прямоугольном треугольнике из вершины угла равного 60, проведена бисектриса длина которой равна 18 см . найдите длину катета, лежащего против данного угла
Другие вопросы по теме Геометрия
Популярные вопросы
- К пружине, массой 200Н/м, прикрепили груз массой 2 кг. Определите...
3 - При каких значениях х трехчлен х2 +10х - 34 принимает зрачение,...
2 - Поясните главную мысль текста своими словами приведите один...
1 - Как найти массу воды, если известна масса раствора и масса вещества?...
3 - Картинка: https://i.imgur.com/8t7PCaV.jpg...
1 - Морфологічний розбір слова без...
1 - ППеречислете природные зоны., где они находятся...
1 - Решить дифференциальное уравнение 2xdy-3ydx=0...
1 - Твір есе Образне слово поетичного модернізму...
2 - До ть будь ласка рішити контрольну роботу з фізики...
1
27 см
Объяснение:
ΔАСМ:
СМ= 9 см (катет лежащий напротив угла в 30° равен половине гипотенузы.)
АС=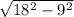
AC=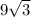
ΔABC:
AC=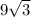
∠B = 30° ⇒
AB=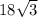 ⇒
⇒
CB=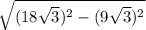
CB=27 см