В прямоугольном треугольнике АВС с катетами АС =16 см и ВС = 12 см и гипотенузой АB = 20 см из вершины B проведена биссектриса BD. Найдите длину BD.

6√5 см

Объяснение:

используем формулу для нахождения длины биссектрисы через катет и гипотенузу

BD = CB ·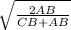 = 12 · 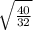= 12 · √5/2 = 6√5 см

Каждая точка биссектрисы равноудалена от сторон угла, DC=DC1

Площади треугольников с равными высотами относятся как основания.

Треугольники ABD и DBC имеют общую высоту из вершины B и равные высоты из вершины D.

SABD/SDBC =AD/DC =AB/BC

Доказали теорему о биссектрисе в случае прямоугольного треугольника.

Биссектриса делит сторону треугольника в отношении прилежащих сторон.

AD/DC =AB/BC =20/12 =5/3

DC =3/8 AC =6

DBC, т Пифагора

BD =√(BC^2 +DC^2) =6√5 (см)

Или

cosB =BC/AB =3/5

cos(B/2) =√((1+cosB)/2) =√(4/5) =2/√5 (B/2 <90)

BD =BC/cos(B/2) =6√5 (см)