В прямоугольном треугольнике ABC проведена биссектриса CE. Перпендикуляр к ней, проходящий через точку E, пересекает катет AC в точке F так, что AF:FC=3:4. Вычислить площадь треугольника ABC, если известно, что длина катета BC равна 56 см. (Впишите целое число)

Ответы

malboro3 12.08.2021 11:04

$\boxed{S_{ABC} = 3920}$ сантиметров квадратных

Объяснение:

Дано: ∠ACB = 90°, ∠ACE = ∠BCE, FE ⊥ CE, AF : FC = 3 : 4, BC = 56 см

Найти: $S_{ABC}$ - ?

Решение: Введем коэффициент пропорциональности x, тогда AF = 3x,

FC = 4x. Так как по условию ∠ACE = ∠BCE и ∠ACE + ∠BCE = ∠ACB, то

∠ACE = ∠BCE = ∠ACB : 2 = 90° : 2 = 45°. Рассмотрим прямоугольный (FE ⊥ CE по условию) треугольник ΔFEC. По теореме про сумму углов треугольника: ∠CEF + ∠FCE + ∠CFE = 180° ⇒ ∠CFE = 180° - ∠CEF - ∠FCE = 180° - 90° - 45°. Так как ∠CFE = ∠FCE = 45°, то по теореме треугольник ΔFEC - равнобедренный, следовательно FE = EC. Пусть CE = y, тогда

FE = y. По теореме Пифагора: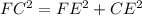 $FC^{2} = FE^{2} + CE^{2}$ .

$(4x)^{2} = y^{2} + y^{2} \\16x^{2} = 2y^{2}|:2\\8x^{2} = y^{2}\\y = x\sqrt{8}$

Проведем высоту к стороне FC из точки E в точку H. Рассмотрим прямоугольный (HE ⊥ FC по построению) треугольник ΔHEC.

$\sin \angle HCE = \frac{HE}{EC} \Longrightarrow HE = EC * \sin \angle HCE = EC * \sin 45^{\circ} = \frac{x\sqrt{8} \sqrt{2} }{2} = \frac{x\sqrt{16} }{2} = \frac{4x}{2} = 2x .$

Так как треугольник ΔFEC - равнобедренный, то по свойствам равнобедренного треугольника высота проведенная к основанию является биссектрисой и медианой, тогда FH = HC = FC : 2 = 4x : 2 = 2x.

AC = AF + FC = 3x + 4x = 7x. AH = AF + FH = 3x + 2x = 5x.

Треугольник ΔAHE подобен треугольнику ΔACB по двум углам так как угол ∠CAB - общий, а ∠AHE = ACB = 90°, тогда по свойству подобных треугольников: $\frac{AC}{AH} = \frac{BC}{HE} \Longrightarrow AC * HE = AH * BC$ .