в правильной треугольной пирамиде сторона основания 4√3 см. Боковое ребро наклонено к плоскости и основанию под углом 30 градусов. Найти объем пирамиды
Другие вопросы по теме Геометрия
Популярные вопросы
- Альфа-частица, влетевшая в камеру Вильсона со скоростью 16 Мм/с,...
1 - Определите ядро какого хим элемента образуется из углерода - 14...
3 - Автобус і вантажна машина, швидкість якої на 16 км/год більша від...
1 - Представь бесконечную приодическую десятичную дробь0.2(34) в виде...
1 - Предположим, фирма имеет следующие характеристики производственного...
2 - Какие тенденции развития мюзикла свидетельствуют о правомерности...
1 - У человека длинные ресницы доминируют над короткими, широкие брови...
1 - с задачами 1. Из точки А к плоскости α проведены перпендикуляр...
1 - Объясните, почему в конце 19- начале 20 века США получили название...
3 - Порушени проблеми в новели Приблуда...
1
Объяснение:
(Смотри вложение)
Формула объёма пирамиды: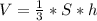 , где:
, где:
S - площадь основания
h - высота пирамиды
Т.к. пирамида правильная ⇒ в основании лежит правильный многоугольник, то есть, в нашем случае, равносторонний треугольник
Формула площади треугольника: SΔ = , где
, где
а - одна сторона
b - соседняя с а сторона
sin α - синус угла между сторонами a и b
Т.к. в основании треугольник равносторонний⇒все углы = 60° и a=b
SΔ =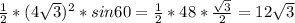
Рассмотрим ΔABC
Т.к. все треугольники равносторонние (т.к. пирамида правильная) ⇒ высота AD является также медианой и биссектрисой. Получается ∠ABC =∠ACB = 60° : 2 = 30° и BD=DC = 4√3 : 2 = 2√3
Рассмотрим ΔADC
По т. Пифагора
AD = √AB²-BD²
AD = √(4√3)²-(2√3)² = √48 - 12 = √36 = 6
Высота пирамиды опускается в точку пересечения биссектрис основания, поэтому HD =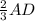 = 4 (Т.к. биссектрисы в точке пересечения делятся 1:2 считая от вершины)
= 4 (Т.к. биссектрисы в точке пересечения делятся 1:2 считая от вершины)
Т.к. все треугольники равносторонние ⇒ высоты у каждого треугольника пирамиды равны, то есть AD = SD
Рассмотрим ΔSHD
ΔSHD - прямоугольный, т.к. SH - высота
По т. Пифагора
SH = √SD²-HD²
SH = √6²-4² = √36-16 = √20 = 2√5
Теперь нам известны все данные для нахождения объёма пирамиды.