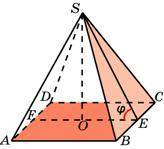
В правильной пирамиде SABCD, все ребра которой равны 1, найдите косинус угла между плоскостями SBC и ABC.

Чтобы найти косинус угла между плоскостями SBC и ABC в данной пирамиде, нам необходимо использовать знания о геометрии и тригонометрии.

1. Для начала, рассмотрим пирамиду ABCD. Она является правильной пирамидой, поэтому все ее ребра равны 1.

2. Мы знаем, что угол между двумя плоскостями равен углу между их нормалями. Таким образом, нам нужно найти нормаль к каждой плоскости и найти угол между ними.

3. Нормаль к плоскости SBC можно получить, найдя векторное произведение векторов SB и SC. В данном случае, SB = [1, 0, 0] и SC = [0, 1, 0]. Вычислим векторное произведение SB и SC:

SB x SC = [1, 0, 0] x [0, 1, 0] = [0, 0, 1]

Таким образом, нормаль к плоскости SBC равна вектору [0, 0, 1].

4. Нормаль к плоскости ABC можно получить, найдя векторное произведение векторов AB и AC. В данном случае, AB = [1, 1, 0] и AC = [1, 0, 0]. Вычислим векторное произведение AB и AC:

AB x AC = [1, 1, 0] x [1, 0, 0] = [0, -1, -1]

Таким образом, нормаль к плоскости ABC равна вектору [0, -1, -1].

5. Теперь, для нахождения косинуса угла между двумя векторами, мы можем использовать формулу: cos(theta) = (A·B) / (|A|·|B|), где A и B - векторы, · обозначает скалярное произведение, |A| и |B| - длины векторов.

6. Длина вектора [0, 0, 1] равна √(0^2 + 0^2 + 1^2) = 1.
Длина вектора [0, -1, -1] равна √(0^2 + (-1)^2 + (-1)^2) = √(2) = √2.

7. Вычислим скалярное произведение векторов [0, 0, 1] и [0, -1, -1]: (0·0 + 0·(-1) + 1·(-1)) = -1.

8. Подставим полученные значения в формулу cos(theta):

cos(theta) = (-1) / (1·√2) = -1 / √2 = -√2 / 2.

Таким образом, косинус угла между плоскостями SBC и ABC равен -√2 / 2.