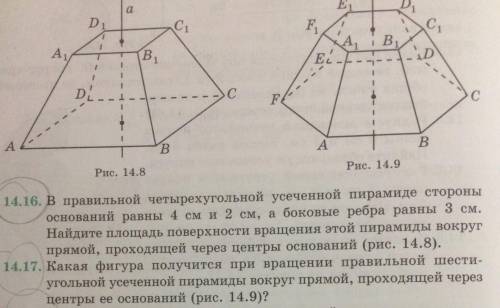
В правильной четырехугольной усеченной пирамиде стороны оснований равны 4см и 2 см, а боковые ребра равны 3см. Найдите площадь поверхности вращения этой пирамиды вокруг прямой, проходящей через центры оснований. какая фигура получится при вращении правильной шестиугольной усеченной пирамиды вокруг прямой, проходящей через центры ее оснований (с объяснением)

Ответ:

Для начала, давайте определим площади оснований этой пирамиды. Так как основания являются правильными четырехугольниками, мы можем использовать формулу площади правильного четырехугольника: S = a^2, где a - длина стороны основания.

Площадь большего основания (S1) будет равна:
S1 = (4см)^2 = 16см^2

Площадь меньшего основания (S2) будет равна:
S2 = (2см)^2 = 4см^2

Теперь, чтобы найти площадь поверхности вращения пирамиды вокруг прямой, проходящей через центры оснований, мы должны найти площадь поверхности каждой грани пирамиды и сложить их.

У пирамиды есть 4 грани, каждая из которых является трапецией. Трапеция - это четырехугольник, у которого две параллельные стороны и две непараллельные стороны, которые встречаются в вершине.

Давайте рассмотрим одну из этих граней. Чтобы найти площадь поверхности этой грани, нам нужно найти площадь боковой поверхности трапеции (Sб) и площадь основания грани (Sосн). Затем мы сложим эти две площади.

Площадь боковой поверхности трапеции можно найти по формуле: Sб = (a + b) * h / 2, где a и b - длины оснований, h - высота трапеции.

В нашем случае, основания трапеции это стороны оснований пирамиды, то есть 4 см и 2 см. Высоту трапеции мы можем найти, используя теорему Пифагора в треугольнике, образованном сторонами боковой грани, одним из оснований и высотой пирамиды. В нашем случае, это треугольник со сторонами 2 см и 3 см. Высоту (h) можно найти, используя формулу теоремы Пифагора: h^2 = 3^2 - 2^2.

Вычисляя, мы получим: h^2 = 9 - 4 = 5, и поэтому h = √5 см.

Теперь мы можем найти площадь боковой поверхности трапеции Sб:
Sб = (4см + 2см) * √5 см / 2 = 6см * √5 см / 2 = 3√5 см^2.

Площадь основания грани (Sосн) будет равна площади большего основания, так как поверхность вращается вокруг прямой, проходящей через центры оснований:
Sосн = S1 = 16см^2.

Итак, площадь поверхности одной грани пирамиды равна сумме площади боковой поверхности трапеции и площади основания:
Sграни = Sб + Sосн = 3√5 см^2 + 16см^2.

Теперь, чтобы найти площадь поверхности вращения пирамиды, нам нужно умножить площадь одной грани на количество граней (4) и добавить площадь оснований:

Sпов = 4 * Sграни + S1 + S2.

Выполним вычисления:
Sпов = 4 * (3√5 см^2 + 16см^2) + 16см^2 + 4см^2
= 12√5 см^2 + 64см^2 + 16см^2 + 4см^2
= 12√5 см^2 + 84см^2.

Поэтому, площадь поверхности вращения этой пирамиды вокруг прямой, проходящей через центры оснований, равна 12√5 см^2 + 84 см^2.

Теперь давайте перейдем ко второй части вопроса, где мы должны найти фигуру, которая получится при вращении правильной шестиугольной усеченной пирамиды вокруг прямой, проходящей через центры оснований.

Шестиугольная пирамида будет иметь шесть равных боковых граней и два равных основания. При вращении пирамиды вокруг прямой, основания станут кругами, а боковые грани станут коническими поверхностями, с каждой из которых будет выступать треугольник.

Таким образом, фигурой, полученной при вращении правильной шестиугольной усеченной пирамиды вокруг прямой, проходящей через центры ее оснований, будет тело вращения, состоящее из двух конических поверхностей и двух круговых оснований.