В правильной четырехугольной усеченной пирамиде сторона большего основания равна 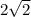, боковое ребро 2, а диагональ осевого сечения . Найдите объем пирамиды

Чтобы найти объем пирамиды, нам нужно знать формулу для вычисления объема пирамиды. Формула для объема пирамиды выглядит следующим образом:

V = (1/3) * S * h,

где V - объем пирамиды, S - площадь основания пирамиды, h - высота пирамиды.

Давайте решим задачу шаг за шагом:

1. Найдем высоту пирамиды (h):
Для этого нам понадобится прямоугольный треугольник, образованный половиной диагонали осевого сечения и половиной бокового ребра пирамиды (изобразим его на бумаге для понятности).

2. По теореме Пифагора найдем длину высоты пирамиды (h):
(h)^2 + (1/2 * 2)^2 = (2sqrt(3))^2,
h^2 + 1 = 12,
h^2 = 11,
h = sqrt(11).

3. Найдем площадь основания пирамиды (S):
Структура пирамиды позволяет нам выделить еще один прямоугольный треугольник на основании пирамиды (соединим его вершину с концом половины диагонали осевого сечения), и тогда получим два прямоугольных треугольника.
Для нахождения площади основания пирамиды мы можем использовать прямоугольный треугольник, образованный сторонами большего основания, половиной диагонали осевого сечения и половиной бокового ребра пирамиды.

4. Найдем площадь треугольника (S):
Используем формулу для площади треугольника:
S = (1/2) * a * b,
где a и b - катеты прямоугольного треугольника.

a = 2sqrt(2), b = 2sqrt(3)/2.

S = (1/2) * 2sqrt(2) * 2sqrt(3)/2,
S = sqrt(6) * sqrt(2),
S = 2sqrt(3).

5. Найдем площадь основания пирамиды (S):
Площадь пирамиды равна площади треугольника умноженной на 2 (так как у нас два таких треугольника на основании пирамиды):
S = 2 * 2sqrt(3),
S = 4sqrt(3).

6. Найдем объем пирамиды (V):
Используем формулу для объема пирамиды:
V = (1/3) * S * h,

V = (1/3) * 4sqrt(3) * sqrt(11),
V = 4sqrt(3) * sqrt(11) / 3,
V = (4 * sqrt(3) * sqrt(11)) / 3,
V = (4 * sqrt(3 * 11)) / 3,
V = (4 * sqrt(33)) / 3.

Таким образом, объем пирамиды равен (4 * sqrt(33)) / 3.