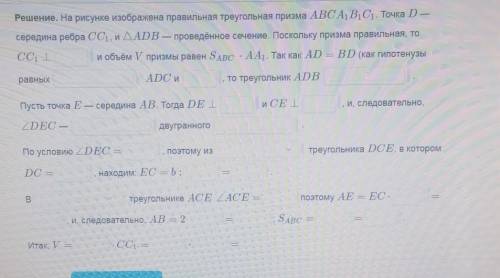
В правильном треугольнике треугольной призме ABC A1 B1 C1 через сторону AB нижнего основания и середину ребра cc1 проведено сечение составляющая с плоскостью основания угол в 30 градусов найти объём призмы если её боковое ребро равно 2 Б Заполнить пропуски
Другие вопросы по теме Геометрия
Популярные вопросы
- На одной чаше весов лежат 6 одинаковых пачек какао и гиря массой 50 грамм , а на...
1 - Разберите слова по составу , в коком из них при- не является приставкой прибыть...
2 - *1. главный строительный материал организма ? 2.самая крупная пищеварительная жклеза?...
1 - Разбор слова по составу слово скрою скроешь...
1 - Ккакому падежу относится слово однажды...
2 - Напишите : распространённые ошибки телеведущих в именах числительных. желательно...
3 - Кто ответит отмечу как лучший и ! ) как определить форму прилагательного? пример:...
2 - It was awfully becoming 1)to 2)with 3)up 4)of...
3 - Вася рассказал друзьям, что позавчера ему ещё было 10 лет, а в следующим году ему...
3 - Между корней лежит уж и всем мне всавить букву...
3
Правильный треугольник - это треугольник, у которого все стороны и углы равны.
Призма - это геометрическое тело, имеющее два основания, которые представляют собой многоугольники, и все боковые грани, которые являются прямоугольниками или параллелограммами.
Сечение - это пересечение двух геометрических фигур, в данном случае плоскость и призма.
Чтобы решить эту задачу, нам понадобится найти высоту призмы и площадь основания для дальнейшего вычисления объема.
1. Найдем высоту призмы:
Рассмотрим треугольник ABC. В правильном треугольнике, медиана, проведенная из вершины к основанию, делит треугольник на два равных равнобедренных треугольника.
Таким образом, высота призмы, которая проходит через сторону AB нижнего основания и середину ребра cc1, равна половине высоты треугольника ABC.
Поэтому, чтобы найти высоту призмы, нужно найти высоту треугольника ABC.
В треугольнике ABC, у нас есть сторона AB, которая равна 2 (дано в условии задачи).
Также известно, что треугольник ABC - правильный, поэтому угол между сторонами AB и AC равен 60 градусов.
Чтобы найти высоту треугольника ABC, мы можем использовать формулу для нахождения высоты правильного треугольника:
высота = (сторона * √3) / 2
Подставляя значения, получаем:
высота = (2 * √3) / 2
высота = √3
Теперь у нас есть высота призмы, которая равна √3.
2. Найдем площадь основания призмы:
Основание призмы представляет собой правильный треугольник ABC.
Площадь основания правильного треугольника можно найти, используя формулу:
площадь = (сторона^2 * √3) / 4
Подставляя значения, получаем:
площадь = (2^2 * √3) / 4
площадь = (4 * √3) / 4
площадь = √3
Теперь у нас есть площадь основания призмы, которая равна √3.
3. Найдем объем призмы:
Объем призмы можно найти, умножив площадь основания на высоту призмы.
объем = площадь * высота
объем = √3 * √3
объем = 3
Ответ: объем призмы равен 3.
Таким образом, объем призмы равен 3.