В параллелограмме АВСD ∠ВСА = 75°, ∠АСD = 60°, АD =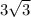 . Найдите АС. решение нужно.

Дано, что в параллелограмме АВСD угол ВСА равен 75°, угол АСD равен 60° и длина стороны АD равна 3√3.

Для решения этой задачи мы можем воспользоваться свойствами параллелограмма. Одно из основных свойств параллелограмма гласит, что противолежащие углы в нем равны. Из этого следует, что угол СDА также равен 75°.

Рисуем параллелограмм:

A
/ \
/ \
/ \
B ------- C
\ /
\ /
\ /
D

Теперь нам нужно найти длину стороны АС.

Когда угол между сторонами параллелограмма известен, можно воспользоваться тригонометрическими соотношениями для нахождения длины стороны.

Мы знаем, что в треугольнике АВС угол В равен 75°, а угол С равен 180° - 75° = 105° (так как сумма углов треугольника равна 180°).

Теперь применяем теорему синусов к треугольнику АВС:

sin(75°) / АС = sin(105°) / АВ

Заменяем знаки синуса на полученные значения:

sin(75°) / АС = sin(105°) / (2 * АД)

Подставляем значения sin(75°) и sin(105°) из таблицы:

√6 - √2 / АС = √2 / (2 * 3√3)

Дальше упрощаем:

√6 - √2 / АС = √2 / (6√3)

Перемножаем крест-накрест:

(√6 - √2) * (6√3) = √2 * АС

6√18 - 6√6 = √2 * АС

Дальше упрощаем:

6 * 3√2 - 6 * √6 = √2 * АС

18√2 - 6√6 = √2 * АС

Делим обе части равенства на √2:

18 - 6√3 = АС

Таким образом, мы получили ответ на задачу: длина стороны АС равна 18 - 6√3.