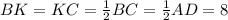В параллелограмме ABCD сторона AD равна 16 см. АК и DK – биссектрисы углов А и D соответственно. Найдите AB (в см)
Другие вопросы по теме Геометрия
Популярные вопросы
- Разложите на множители 12xy-3y+4x^2-x...
1 - Откройте графический редактор по работе с векторными изображениями....
2 - Спортивное соревнование 10 предложений...
2 - 10 класс хэлп запишите необходимые условия для смещения равновесия в...
3 - Эссе на тему водно-солевой в организме человека...
1 - Найдите значения выражения 0,6(в кубе)-2*0,6(в квадрате)*0,8+0,6*0,8(в...
2 - Привилегии и запреты для членов тевтонского ордена...
3 - Каким предстоёт петербург в повести шинкль?...
3 - 1представь себе,что ты создатель робота.подумай какие функции ты бы...
2 - Проверти правильность написания предложений, и исправте ошибки!...
1
ответ: 8
Объяснение:
∠DKC=∠KDA (накрест лежащие секущей KD пересекающей параллельные прямые BC и AD)
А по условию ∠KDA=∠KDC (DK - биссектриса)
Следовательно ΔKDC равнобедренный и KC=CD
∠BKA=∠KAD (накрест лежащие секущей AK пересекающей параллельные прямые BC и AD)
А по условию ∠KAD=∠KAB (AK - биссектриса)
Следовательно ΔABK равнобедренный и BK=AB
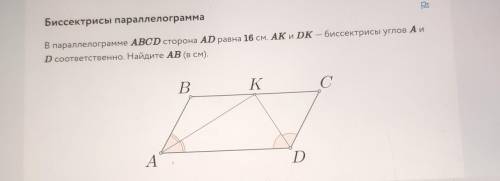
В параллелограмме противоположные стороны равны и AB=CD, откуда следует, что и BK=KC.
Следовательно