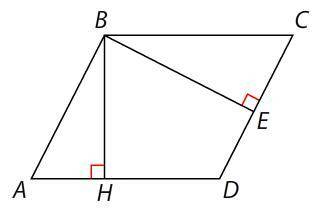
В параллелограмме ABCD ∠A = 30°, BH = 4 см, BE = 6 см. Найдите площадь параллелограмма. ответ дайте в квадратных сантиметрах. с решением
Другие вопросы по теме Геометрия
Популярные вопросы
- Снаряд масою 25кг, що летить горизонтально зі швидкістю 250м/с, попадає у вагонетку...
1 - Почему во времена советской власти политические репрессии постоянно повторялись?...
1 - Что такое анимизм А) вера в духов и души В) Вера в силы природы С) Вера в силу...
2 - номер заранее очень при очень за 20 минут...
3 - Виконати завдання до тексту. ТЕКСТ 1) Стояв квітень ми жили в Ялті байдикували...
2 - Кут між діагоналями рівнобедреної трапеції дорівнює 120° . Висота трапеції -10...
3 - Сравнить экономическую политику Александра II и Александра III...
1 - Короткий паспорт-характертстику М.Булгакова Собаче Серце ...
2 - Л. Толстой утверждал: Чтобы жить честно, надо рваться, путаться, биться, ошибаться,...
1 - 1.There are/is some coffee in the cup2.We haven t got some/any eggs in the fridge3.How...
2
Первым шагом нам нужно выразить площадь параллелограмма через известные нам данные. Известно, что высота параллелограмма (отрезок BH) равна 4 см, а основание (отрезок AD) равно 6 см.
Площадь параллелограмма равна произведению длины основания на высоту, то есть S = AD * BH.
Вторым шагом нам нужно найти длину основания AD. Мы знаем, что параллелограмм ABCD - это параллелограмм, а значит, противоположные стороны равны. Это означает, что сторона AD имеет такую же длину, как сторона BC. Мы знаем, что сторона BE равна 6 см, а угол B = 30°.
Для нахождения длины стороны BC, воспользуемся теоремой косинусов:
BC^2 = BE^2 + EC^2 - 2 * BE * EC * cos(B)
Подставим известные значения и рассчитаем:
BC^2 = 6^2 + 4^2 - 2 * 6 * 4 * cos(30°)
BC^2 = 36 + 16 - 48 * 0.866 (косинус 30° равен 0.866)
BC^2 = 52 - 41.568
BC^2 = 10.432
Теперь найдем длину стороны BC:
BC = sqrt(10.432)
BC ≈ 3.23 см
Итак, мы нашли длину основания AD, которая равна длине стороны BC, и получили, что AD ≈ 3.23 см.
Теперь мы можем вычислить площадь параллелограмма:
S = AD * BH
S ≈ 3.23 см * 4 см
S ≈ 12.92 см^2
Итак, площадь параллелограмма равна примерно 12.92 квадратных сантиметра.