В основании прямой призмы лежит ромб с диагоналями, равными 10 и 24. Площадь ее поверхности равна 344. Найдите боковое ребро этой призмы.

2

Объяснение:

Sосн=1/2*10*24=120 площадь ромба

Sпол=2Sосн+Sбок

Sбок=Sпол-2Sосн=344-(2*120)=344-240=

=104. площадь боковой поверхности призмы

Диагонали ромба пересекаются перпендикулярно и точкой пересечения делятся пополам

По теореме Пифагора найдем сторону ромба

√((24/2)²+(10/2)²)=√(576/4+100/4)=

=√(144+25)=√169=13

Росн=4*13=52 периметр ромба

Sбок=Росн*h

h=Sбок/Росн=104/52=2 боковое ребро

ответ: 2

Объяснение:

, где

Sп.п - площадь полной поверхности

Sосн. - площадь основания

Sбок - площадь боковой грани

Рассмотрим основание призмы

Мы можем узнать сторону основания(понадобиться позже). Тк. по свойству ромба его диагонали перпендикулярны и делятся пополам, то ромб разбит на 4 равных прямоугольных треугольника с катетами 5 и 12. Рассмотрим 1 из них.

По т. Пифагора:

Площадь ромба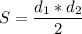

Подставляем в формулу площади полной поверхности призмы

Мы знаем, что боковая грань - прямоугольник,т.е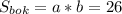  

Т.к. нам известна одна из сторон(сторона основания, которая равна 13), то мы можем найти и боковое ребро