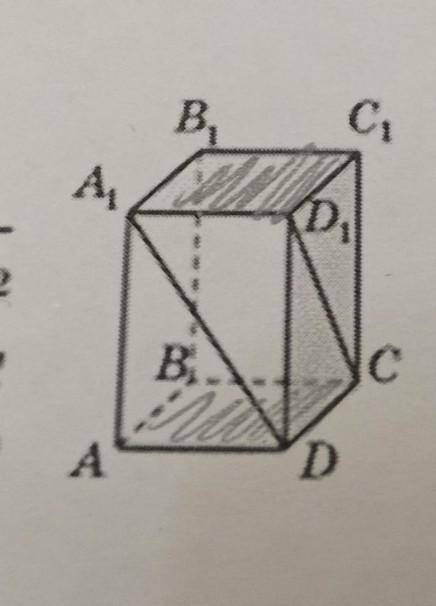
В основании прямоугольного параллелепипеда лежит квадрат ABCD с площадью 36 см2 (рис. 270). Периметр треугольника DD1C
равен 24 см. Диагональ A1D грани AA1D1D
равна 10 см. Найдите площадь поверхности параллелепипеда.
(7 класс)​

Добрый день! Для решения задачи, нам нужно найти площадь поверхности параллелепипеда. Для этого выделим все грани параллелепипеда и найдем их площади, а затем сложим эти площади. 1. Начнем с основания параллелепипеда, которое является квадратом ABCD. У нас уже есть информация, что его площадь равна 36 см². 2. Теперь у нас есть треугольник DD₁C, у которого известен периметр и одна из его диагоналей. Для нахождения площади этого треугольника, нам нужно знать длину его основания и высоту. a. Периметр треугольника равен 24 см. Периметр это сумма длин всех сторон треугольника. Из условия задачи, мы знаем, что сторона DC равна стороне AB, которая, в свою очередь, является стороной квадрата ABCD. Таким образом, периметр треугольника можно представить как 4 * длина стороны DC. b. Выразим длину стороны DC через сторону квадрата ABCD. Пусть сторона квадрата ABCD равна а. Тогда периметр треугольника можно записать как 4 * a = 24 см. c. Решая это уравнение, мы находим, что длина стороны квадрата равна a = 6 см. d. Теперь, когда у нас есть длина стороны квадрата ABCD, мы можем найти "высоту" треугольника DD₁С. Высота это отрезок, опущенный из вершины DD₁ на основание СС₁. Мы можем найти эту высоту с помощью теоремы Пифагора или применив теорему Пифагора к прямоугольному треугольнику АА₁D. e. У нас есть гипотенуза AD₁ = 10 см и один катет АА₁ = а/√2 = 6/√2 (так как сторона квадрата ABCD равна а = 6 см). f. По теореме Пифагора находим второй катет: √(AD₁² - АА₁²) = √(10² - (6/√2)²) = √(100 - 36/2) = √(100 - 18) = √82. g. Получили высоту треугольника DD₁C равную √82 см. h. Теперь, когда у нас есть основание треугольника DD₁C равное 24 см и высота √82 см, мы можем найти его площадь S DD₁C = (основание * высота) / 2 = (24 * √82) / 2 = 12√82 см². 3. Посчитаем площадь боковых граней параллелепипеда. На параллелепипеде есть 4 боковые грани, и они являются прямоугольниками. Длина каждой боковой грани равна стороне AB квадрата ABCD, то есть 6 см. Ширина каждой боковой грани равна высоте треугольника DD₁C, то есть √82 см. Таким образом, площадь каждой боковой грани равна (длина * ширина) = 6 * √82 = 6√82 см². 4. Теперь, чтобы найти площадь поверхности параллелепипеда, мы должны сложить площади всех его граней. Площадь поверхности S параллелепипеда = 2 * (площадь основания + площадь боковой грани) = 2 * (36 + 12√82 + 6√82) = 2 * (36 + 18√82) = 72 + 36√82 см². Таким образом, площадь поверхности параллелепипеда равна 72 + 36√82 см².