В окружность с радиусом 4 корень из 3 см вписан правильный треугольник,
a) найдите сторону треугольника
в)вычислите площадь круга вписанного в этот треугольник
Другие вопросы по теме Геометрия
Популярные вопросы
- Орны ауысқан сөздерді дұрыс орналастырып, сөйлем құрастыр. Сөйлемдерден...
3 - Р, Упражнение 220) Со словами из рамок (стр. 96) составьте и за-пишите...
2 - План до твору острів хортиця...
2 - 80*1/5=16 маленьких грифелей 80-16=64 больших грифелей16*9 см 5мм=16*9,5см=152...
3 - Дано: c1=9; cn+1=2cn+8 найдите c5...
2 - (слон кошка зебра) сделай с ними подежи как в фото мама поругает если...
1 - это 2 класс там два номера!...
1 - Як впливають конфлікти на стосунки і здоров я людей?...
2 - 3x-7 x+1;2+x 8-x;1-x 2x-5;2x+1 x+6;4x+2 3x+1;6x+1 2x+9....
3 - На страницае 152 по русскому Пуськи бятые как сделаи ...
3
1)а=R*корень из 3=4 корень из 3*корень из 3=12см
2)S(круга) =пR^2=п*(4 корень из 3) ^2=48п
36π или 113,095
Объяснение:
Т.К. треугольник правильный, то центр окружности находится на пересечении биссектрис ⇒ ∠ABO = ∠BAO = 30° ⇒ ∠AOB=180°-∠BAO -∠ABO = 120°
По теореме косинусов
a² = AO²+BO² - 2*AO*OB*cos∠120°=2*48 -48
a=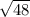
r₂ =√(r₁²- ( )²) =
)²) =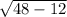 =6
=6
S=πr²=36π