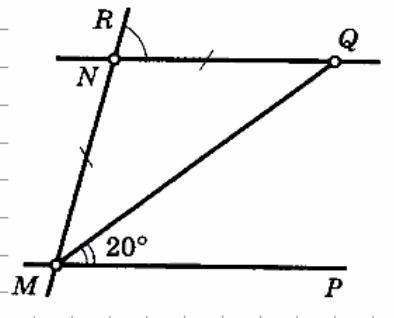
в этой задаче. Нужно доказать параллельность прямых NQ и MP.

Для доказательства параллельности прямых NQ и MP, мы можем использовать свойство, что если две прямые пересекаются с третьей прямой таким образом, что сумма внутренних углов на одной стороне равна 180 градусам, то эти прямые параллельны.

Итак, нам нужно найти два угла, сумма которых равна 180 градусам, чтобы доказать параллельность NQ и MP.

Обратим внимание на следующие факты:
- Из условия задачи мы знаем, что угол MQP равен 63 градусам, а угол PQN равен 117 градусам.
- Также, угол PNM является вертикальным углом к углу PQN, поэтому он также равен 117 градусам.

Теперь мы можем приступить к доказательству. Для этого мы будем использовать теорему о параллельных прямых, которая говорит нам, что если в треугольнике одна сторона параллельна одной из сторон другого треугольника, а две другие стороны пересекаются, то треугольники подобны.

В нашем случае мы рассмотрим треугольники MQP и PQN. У нас уже есть одна пара равных углов (углы MQP и PQN). Также, у нас есть еще одна пара равных углов (углы PNM и PQN). Это достаточно для доказательства подобности треугольников.

Исходя из подобия треугольников MQP и PQN мы можем сделать следующие выводы:
- Соответствующие углы треугольников равны (углы QMP и QPN).
- Соответствующие стороны треугольников пропорциональны.

Теперь, обратим внимание на стороны MQ и PN. Если мы предположим, что NQ и MP параллельны, то у нас есть две пары параллельных сторон (MQ и PN, NQ и MP), а значит третья пара сторон - QM и NP, также будет параллельна.

Таким образом, мы доказали, что прямые NQ и MP параллельны.