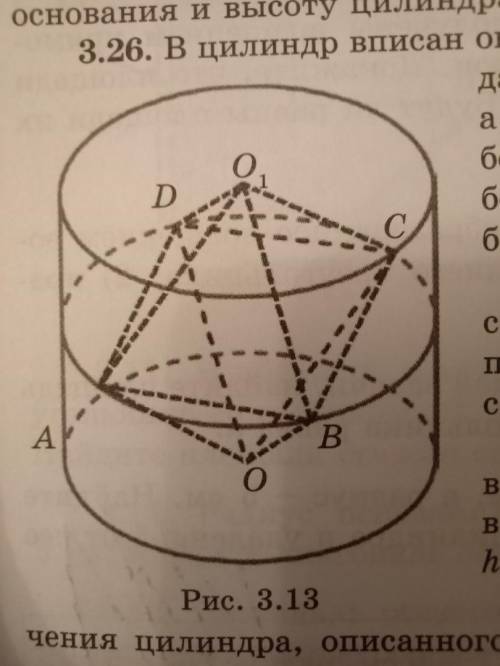
В цилиндр вписан октаэдр так, что две его вершины совпадают с центрами оснований цилиндра, а другие его вершины расположены на боковой поверхности. Найдите площадь боковой поверхности цилиндра, если ребро октаэдра равно а.

В цилиндр вписан октаэдр так, что две его вершины совпадают с центрами оснований цилиндра, а другие

Ответы

aknietzhumanova 25.02.2021 20:00

площадь боковой поверхности цилиндра:

$s = 2 \pi \: {a}^{2}$

Объяснение:

диагонали октаэдра равны.

=> диаметр цилиндра = высоте цилиндра.

диаметр и высоту цилиндра найдем как диагональ квадрата ABCD

$d = a \sqrt{2} \\ h = a \sqrt{2}$

площадь боковой поверхности цилиндра:

$s = 2\pi \: rh = \pi \: dh$

$s = \pi \times a \sqrt{2} \times a \sqrt{2} = 2\pi \: {a}^{2}$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

azlidenp08oin 14.12.2020 20:40

Masha6655 14.12.2020 20:44

Сор по геометрии 7класс выбрал 30б( номер 3,4)...

goe1 13.04.2020 06:27

N(-5:-70) M(0;-69) найти абсциссу...

Rollov35 13.04.2020 06:27

elenarum18 13.04.2020 06:27

Решить задачи с 1 по 10, они в одно действие...

nara01072003 20.07.2019 12:30

FireStreamGun 18.06.2020 13:55

Gumashova 18.06.2020 13:58

kirilll2233 21.04.2021 10:22

Cheburek1112 21.04.2021 10:22