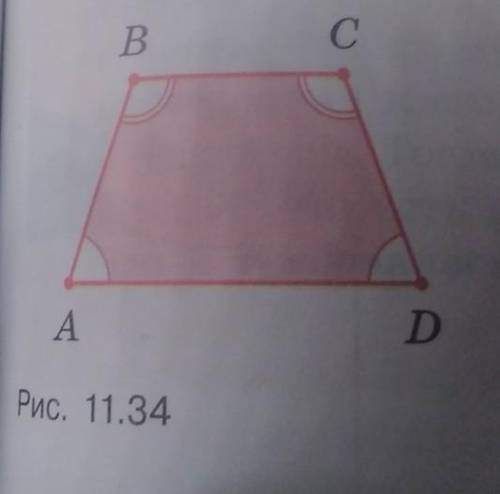
В четырехугольнике ABCD угол А равен углу D, а угол В равен углу С, причем, прямые АВ и CD не параллельны (рис. 11.34). Докажите, что АВ=CD​

Чтобы доказать, что AB=CD, мы можем использовать свойство треугольников, а именно то, что сумма углов треугольника равна 180 градусам.

1. Рассмотрим треугольник ABD. Угол ABD равен углу D, так как это указано в условии задачи. Также у нас есть угол BAD, который равен углу C по условию. Следовательно, углы ABD и BAD равны между собой.

2. Рассмотрим треугольник BCD. Угол BCD равен углу C, так как это указано в условии задачи. Также у нас есть угол BCD, который равен углу A по условию. Следовательно, углы BCD и CDB равны между собой.

3. Из пунктов 1 и 2 следует, что угол BAD равен углу CDB.

4. Добавим отрезки AD и BC к нашей фигуре. Мы получим два треугольника: треугольник ABD и треугольник CDB.

5. Так как угол BAD равен углу CDB, а угол ABD равен углу CBD, то у нас получаются два подобных треугольника.

6. Из свойств подобных треугольников следует, что соответствующие стороны этих треугольников пропорциональны. В нашем случае это означает, что AB/CD = AD/BC.

7. Мы знаем, что угол В равен углу С (по условию задачи). Так как AB/CD = AD/BC, то это означает, что угол А равен углу D. Но мы уже знаем, что это верно по условию задачи. Следовательно, наши треугольники не только подобны, но и равны.

8. Значит, стороны AB и CD равны друг другу. Таким образом, мы доказали, что AB=CD.

Все вышеперечисленные шаги можно изобразить на рисунке и объяснить школьнику, чтобы он мог понять логику решения задачи.