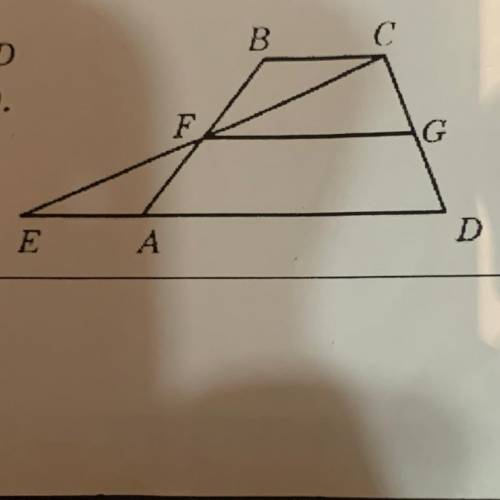
В четырёхугольнике ABCD FB=FA, FC=FE, FG ||AD. Докажите, что FG||BC

Добрый день! Я рад выступить в роли вашего школьного учителя и помочь вам решить эту задачу.

Для начала, давайте взглянем на данную нам информацию и изобразим ее на рисунке.

Мы знаем, что в четырехугольнике ABCD, отрезки FB и FA равны, а отрезки FC и FE тоже равны. Также, мы знаем, что отрезок FG параллелен отрезку AD.

Для доказательства того, что отрезок FG параллелен отрезку BC, мы можем воспользоваться свойством параллельных прямых. Оно утверждает, что если две прямые пересекаются третьей прямой таким образом, что уголы между ними (между пересекающимися прямыми и третьей прямой) равны, то эти две прямые параллельны.

Вернемся к нашей задаче. Мы должны доказать, что FG параллелен BC. Для этого нам нужно установить, что углы между FG и BC равны.

Давайте рассмотрим треугольники AFB и CFE. Из условия задачи мы знаем, что отрезки FB и FA равны, а отрезки FC и FE тоже равны. Значит, эти треугольники равны по двум сторонам и углу, поскольку стороны и угол против левой стороны по этому углу равны между собой.

Теперь рассмотрим углы GFB и CED. Отрезок FG параллелен отрезку AD, поэтому угол GFB и угол CED являются соответственными углами и равны между собой.

Вспомним свойство параллельных прямых: если углы между пересекающимися прямыми и третьей прямой равны, то эти две прямые параллельны.

Мы вычислили, что углы GFB и CED равны, следовательно, прямые FG и BC параллельны.

Таким образом, мы доказали, что отрезок FG параллелен отрезку BC.

Надеюсь, я смог объяснить вам данную задачу подробно и понятно. Если у вас остались вопросы или вам нужно больше объяснений, пожалуйста, сообщите мне. Я всегда готов помочь вам в учебе!

Объяснение:

Рассмотрим Δ АВС и ΔАСД:

Стороны АВ=СД, ВС=АД - равны по условию задачи ;

Сторона АС - общая сторона Δ АВС и Δ АДС;

Следовательно, ΔАВС = ΔАСД - по 3 признаку равенства треугольников (по трём сторонам)