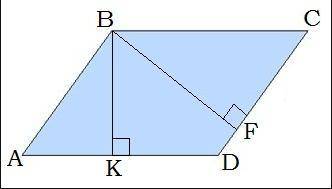
УМОЛЯЮ Дано:
CD= 13 см;
AD= 9 см;
BK=7 см.

Найти: S(ABCD).

ответ: площадь параллелограмма ABCD равна см2.

Добрый день!

Для решения этой задачи, нам понадобится использовать знания о площади параллелограмма. Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны. Также, мы знаем, что площадь параллелограмма вычисляется как произведение длины одной из сторон на высоту, опущенную к этой стороне.

В данной задаче, нам даны следующие данные:

CD = 13 см (длина стороны CD),
AD = 9 см (длина стороны AD),
BK = 7 см (длина стороны BK).

Мы хотим найти площадь параллелограмма ABCD (S(ABCD)).

Чтобы решить эту задачу, мы можем воспользоваться свойством параллелограмма, согласно которому, диагонали параллелограмма делятся пополам. Это означает, что точка пересечения диагоналей (точка K на данной диаграмме) делит каждую диагональ пополам. То есть, DK = KC и AK = KB.

Для нашей задачи, нам дано, что DK = KC = 6 см (поскольку BK = 7 см, то DK и KC равны половине BK = 7/2 = 3.5 см).

Теперь мы можем использовать полученные данные, чтобы найти высоту параллелограмма. Высота параллелограмма - это расстояние между сторонами, которое проведено перпендикулярно к этим сторонам.

Мы можем провести высоту от точки K к стороне AD (так как BK и AD являются параллельными сторонами параллелограмма). Обозначим это расстояние как h.

Теперь у нас есть два треугольника внутри параллелограмма: ADC и BKC, и мы можем использовать свойства треугольников.

В треугольнике ADC у нас есть две стороны, CD и AD, которые известны нам: CD = 13 см и AD = 9 см.

Мы можем воспользоваться теоремой Пифагора для нахождения третьей стороны. Теорема Пифагора утверждает, что квадрат длины гипотенузы (самой большой стороны треугольника) равен сумме квадратов длин двух остальных сторон.

Таким образом, в треугольнике ADC, мы можем применить теорему Пифагора:

AC^2 = AD^2 + CD^2
AC^2 = 9^2 + 13^2
AC^2 = 81 + 169
AC^2 = 250
AC = √250 ≈ 15.811 см

Теперь, чтобы найти высоту, нам понадобится использовать треугольникы BKC и AKC. Заметим, что эти два треугольника подобны (имеют одинаковые углы), поскольку у них одна общая сторона BK и две параллельные стороны (CK и AK). Поэтому отношение длин сторон этих треугольников равно отношению соответствующих сторон:

BK/AK = CK/AC

Подставим известные значения:

7/AK = 3.5/15.811

Теперь мы может решить это уравнение относительно AK:

AK = (7 * 15.811) / 3.5 ≈ 31.578 / 3.5 ≈ 9 см.

Таким образом, высота параллелограмма, проведенная от точки K к стороне AD, равна 9 см.

Теперь, когда у нас есть высота и длина одной из сторон параллелограмма, мы можем вычислить его площадь, используя формулу площади параллелограмма:

S = сторона * высота

S(ABCD) = AD * h
S(ABCD) = 9 * 9
S(ABCD) = 81 см^2

Таким образом, площадь параллелограмма ABCD равна 81 квадратным сантиметрам.