УМОЛЯЮ Дан равнобедренный треугольник. Найдите отношение радиусов вписанной и описанной окружностей, если : угол при вершине равен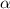
2) Дан выпуклый четырехугольник. Отрезки, соединяющие середины противоположных сторон, равны 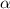и и пересекаются под углом 60 градусов
3) Докажите что углы треугольника ABC связаны соотношением: sin² ∠A+sin²∠B-sin²∠C=2sin∠Asin∠Bcos∠C.
4) Дан прямоугольник ABCD. Докажите, что для любой точки O выполняется равенство: вектор OA · вектор OC = вектор OB · вектор OD.
5) Даны произвольные точки A, B, C и D. Докажите равенство: вектор AB · вектор OC + вектор AD · вектор BC - вектор AC · вектор BD = 0.

elizka070408    1   23.12.2020 07:03    11