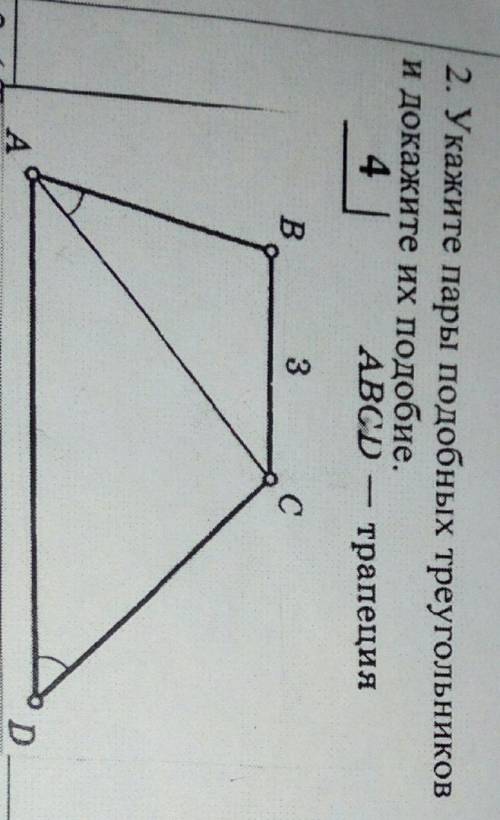
Укажите пары подобных треугольников и докажите их подобие. ABCD - трапеция

На рисунке показана трапеция ABCD. Нам нужно найти пары подобных треугольников и доказать их подобие.

Подобные треугольники имеют одинаковые соотношения сторон и углов. То есть, если мы найдем два треугольника, в которых соотношения сторон и углов одинаковы, то мы можем сказать, что они подобны.

На рисунке трапеции ABCD мы можем найти несколько пар подобных треугольников:

1. Треугольник ABC и треугольник ADC. Оба треугольника имеют общую сторону AD и общий угол при D. Также соотношения длины сторон в этих треугольниках равны: AB/AD = BC/CD. Значит, треугольники ABC и ADC подобны.

2. Треугольник ABD и треугольник CBD. В этих треугольниках общая сторона - BD и общий угол при B. Также соотношения длины сторон в этих треугольниках равны: AB/BC = AD/DC. Значит, треугольники ABD и CBD подобны.

Теперь нам нужно доказать подобие каждой пары треугольников.

1. Доказательство подобия треугольников ABC и ADC:

Мы знаем, что AB/AD = BC/CD. Нам нужно показать, что соотношение углов также одинаково.

У нас есть две пары равных углов: ∠ABC = ∠ADC (по условию - это общий угол D) и ∠CAB = ∠CAD (вертикальные углы).

Следовательно, соотношение углов также совпадает, и треугольники ABC и ADC подобны.

2. Доказательство подобия треугольников ABD и CBD:

Мы знаем, что AB/BC = AD/DC. Нам нужно показать, что соотношение углов также одинаково.

У нас есть две пары равных углов: ∠ABD = ∠CBD (по условию - это общий угол B) и ∠BAD = ∠BDC (вертикальные углы).

Следовательно, соотношение углов также совпадает, и треугольники ABD и CBD подобны.

Таким образом, мы доказали, что треугольники ABC и ADC, а также треугольники ABD и CBD, подобны на основании равенства соотношений сторон и углов.