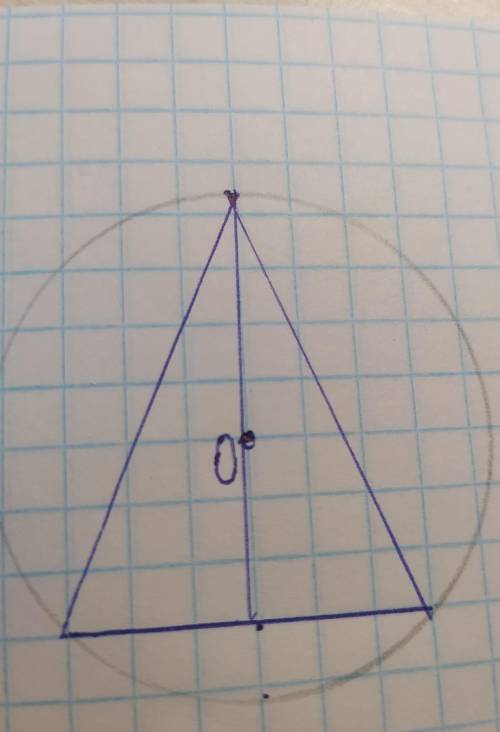
‼️ У трикутнику центр ОПИСАНОГО кола лежить на висоті. Доведіть що цей трикутник рівнобедренний
Другие вопросы по теме Геометрия
Популярные вопросы
- Решите уравнение: log9x=2 решите подробно, буду !...
2 - Существует ли зависимость между временем движения t и пройденным за...
3 - Программа запрашивает у пользователя числа а,б,с. далее происходит решение...
1 - Сделайте схему просто ( сам синтакс разбор не надо) охотники вздрогнули...
2 - Найдите первообразные для функций: 10x, x в квадрате, sin x в квадрате,...
3 - Найдите производную f (x)=из под корня x-2...
3 - Найти производную f (x)=из под корня x-2...
2 - Найти производную функции y=(x^2+3x)^5...
2 - Выразите: 4565 мм=. найдите значение выражения: 60-(13+2): 5-6-3+25=...
1 - Втреугольнике abc известно, что ac =16, bc= 12 ∠ с равен 90°. найдите...
3
Центр кола, яке вписане у трикутник, знаходиться у точці перетину бісектрис.
Отже, BN—бісектриса.
Якщо BN—висота і бісектриса, то з цього випливає, що трикутник ABC—рівнобедренний.
Объяснение:
Центр окружности описанной около треугольника-точка пересечения серединных перпендикуляров его сторон.
AD⊥BC, O∈AD⇒AD-серединный перпендикуляр отрезка BC
Тогда BD=CD, значит AD-медиана
AD-медиана, AD-высота⇒ΔАBC-равнобедренный
ч.т.д.