Тупий кут прямокутної трапеції дорівнює 150°, менша основа √3 см, більша бічна сторона 4см . Знайти площу трапеції .​

4√3 см²

Объяснение:

Проведемо висоту РН. тоді ∠МРН=90°, ∠ТРН=150-90=60°

Розглянемо ΔТРН - прямокутний, ∠Т=90-60=30°

РН=¹/₂ РТ за властивістю катета, що лежить навпроти кута 30°

РН=2 см

ТН=√(РТ²-РН²)=√(16-4)=√12=2√3 см

КН=МР=√3

КТ=КН+ТН=2√3+√3=3√3 см

S(КМРТ)=(МР+КТ)/2*РН=(3√3+√3)/2*2=2√3*2=4√3 см²

Відповідь:

4*√3 см^2

Пояснення:

Оскільки тупий кут прямокутної трапеції-150°, то гострий кут 180°-150°=30°. Проведемо висоту СК (дивитися документ). Тоді кут KCD= 90°-30°=60°. Тоді CK=1/2CD=2 cм (за властивістю катета, що лежить проти кута 30°). Тоді KD=CD*cos30°=CD*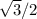=2*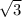см. Тоді більша сторона AD=KD+BC=√3+2*√3=3*√3. Тоді площа прямокутника AKCB=AK*CK=2*√3 cм^2. Площа трикутника KCD =CK*KD/2=2*2*√3/2=2*√3 см^2

Площа трапеції- це сума площі трикутника і прямокутника, тобто 2*√3+2*√3=4*√3 см^2