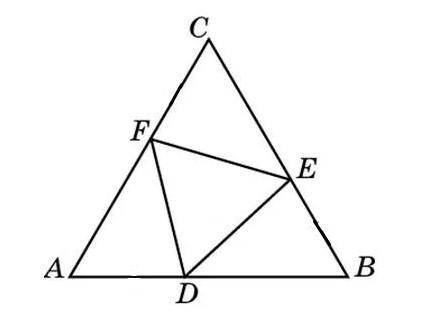
Треугольники ABC и DEF равносторонние. Докажите, что AD=BE=CF
Другие вопросы по теме Геометрия
Популярные вопросы
- Фізики розуміють, щ зелений колір у рослин - це не випадково, адже найктивніше...
3 - Для спортивного выступления гимнасток построились в ряды так что в первом...
3 - Прочитай четверостишие .спиши.обозначть падеж выделенных имён существительных...
2 - 1) что называется прямой речью 2 ) какие знаки ставятся при прямой речи...
2 - 25 что объединяет слова в каждом ряду и почему ты так решил (1 предложение)....
2 - За три дня в классе выполнили 15 по .из них в первый день было выполнено...
3 - Составьте словосочетания со словами шалость, колос, тоска, слить...
3 - Вопросы к слову свиток так,чтобы они были связаны с религиями?...
1 - Скажите проверочное слово к слову семечками на 2 букву е...
1 - Как переводиться слово cookery lessons...
1
Объяснение:
как я понел завтра на улице дождь, удачи
как я понел завтра на улице дождь, удачи
как я понел завтра на улице дождь, удачи
как я понел завтра на улице дождь, удачи
как я понел завтра на улице дождь, удачи
как я понел завтра на улице дождь, удачи
как я понел завтра на улице дождь, удачи
как я понел завтра на улице дождь, удачи
как я понел завтра на улице дождь, удачи
Из условия задачи мы знаем, что треугольники ABC и DEF являются равносторонними. Это означает, что все стороны этих треугольников равны между собой.
Обозначим стороны треугольника ABC как AB, BC и CA, а стороны треугольника DEF как DE, EF и FD.
1. Рассмотрим треугольник ABC. У него все стороны равны между собой, значит AB=BC и BC=CA.
2. Теперь рассмотрим треугольник DEF. У него также все стороны равны между собой, значит DE=EF и EF=FD.
3. Из условия задачи также известно, что треугольники ABC и DEF равносторонние. Это значит, что их стороны соответственно равны между собой: AB=DE, BC=EF и CA=FD.
4. Теперь мы можем сделать выводы. Рассмотрим сторону AD треугольника DEF. По пункту 3, эта сторона равна стороне BC треугольника ABC: AD=BC.
5. Рассмотрим сторону BE треугольника DEF. По пункту 3, эта сторона равна стороне CA треугольника ABC: BE=CA.
6. Рассмотрим сторону CF треугольника DEF. По пункту 3, эта сторона равна стороне AB треугольника ABC: CF=AB.
Таким образом, мы получили, что AD=BC, BE=CA и CF=AB. Но мы знаем из пункта 1, что AB=BC и из пункта 2, что BC=CA. Поэтому, по транзитивности равенства, мы можем сказать, что AD=BE=CF.
Итак, мы доказали, что в равносторонних треугольниках ABC и DEF стороны, соединяющие вершины с одинаковым номером (AD, BE, CF), равны между собой."