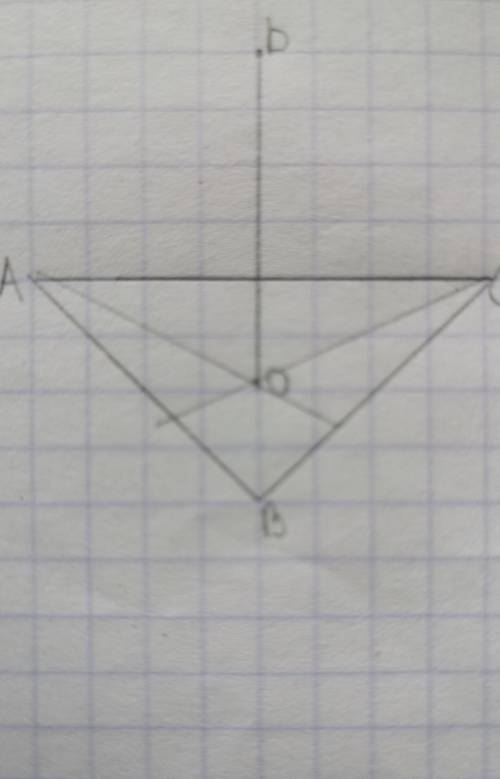
Треугольник Авс-правильный,DO=8,DO перпендикулярна(Авс),ВС=6корней3.Найти АD
Другие вопросы по теме Геометрия
Популярные вопросы
- Какая масса 3%-ого раствора серной кислоты полностью прореагирует...
3 - Напишите уравнение реакции образования полного сложного эфира из...
3 - Дана таблица распределения частот использования терминала банкомата...
3 - Жол белгілері мен сигналдары» туралы конвенция Қазақстанда қай жылы...
3 - Даны точки A(1; 3), B(-4; -5), C(-3; 1), Д(2; -4). Изобразите их...
2 - Заполните сравнительную таблицу социально-экономических и политических...
2 - Write TRUE or FALSE: Example: The earthquake that hit Haiti was...
2 - Укажите вещество с ковалентной связью укажите вещество с ковалентной...
1 - You are asked to write an article with the title Tourism in Kazakhstan...
2 - 5. Площадь малого поршня гидравлической машины 15 см2, а площадь...
2
AD=10
Объяснение:
AO=R.
R=BC/√3
AO=BC/√3=6√3/√3=6 ед
∆АOD- прямоугольный треугольник
По теореме Пифагора
АD=√(AO²+DO²)=√(8²+6²)=√(64+36)=√100=
=10 ед
Рассмотрим треугольник АВС. У него АВ = ВС, так как он является правильным треугольником.
Зная, что ВС = 6 * корень из 3, мы можем выразить АВ через ВС:
АВ = ВС = 6 * корень из 3
Теперь рассмотрим треугольник АОВ. Он является равнобедренным треугольником, так как АВ = ВО.
Половина основания треугольника АОВ - это прямая ОD. Мы знаем, что ОD = 8. Поэтому ВО = 2 * ОD = 2 * 8 = 16.
Теперь мы можем найти другую сторону равнобедренного треугольника АОВ, используя теорему Пифагора:
АО в квадрате = ВО в квадрате - ОА в квадрате
АО в квадрате = 16 в квадрате - ОА в квадрате
АО в квадрате = 256 - ОА в квадрате
ОА в квадрате + АО в квадрате = 256
2 * АО в квадрате = 256
АО в квадрате = 256 / 2
АО в квадрате = 128
Таким образом, ОА = корень из 128 = 8 корень 2.
Вопрос состоит в том, чтобы найти АD. Мы можем использовать теорему Пифагора для треугольника АДО:
АД в квадрате = АО в квадрате - ОД в квадрате
АД в квадрате = (8 корень 2) в квадрате - 8 в квадрате
АД в квадрате = 64 * 2 - 64
АД в квадрате = 128 - 64
АД в квадрате = 64
Таким образом, АД = корень из 64 = 8.
Ответ: АД = 8.