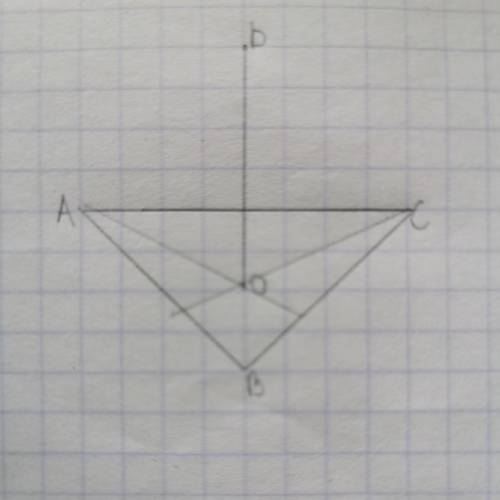
Треугольник Авс-правильный,DO=8,DO перпендикулярна(Авс),ВС=6корней3.Найти АD​

Для решения данного вопроса, мы можем использовать свойства правильных треугольников и применить теорему Пифагора.

Во-первых, у нас есть информация, что треугольник АВС является правильным. Это означает, что все его стороны равны между собой. Таким образом, мы можем сказать, что AV = BV = СV = 6√3 (корень из 3).

Затем, мы имеем информацию, что OD = 8 и OD перпендикулярно стороне АВС. Это означает, что треугольник ODA является прямоугольным.

Мы можем использовать теорему Пифагора, чтобы найти значение стороны AD. Теорема Пифагора гласит, что для прямоугольного треугольника с гипотенузой (стороной противоположной прямому углу) c и катетами (сторонами прилегающими к прямому углу) a и b, справедливо a^2 + b^2 = c^2.

Применяя эту теорему к треугольнику ODA, мы можем записать:

AD^2 + OD^2 = OA^2

AD^2 + 8^2 = AV^2

AD^2 + 64 = (6√3)^2

AD^2 + 64 = 108

AD^2 = 108 - 64

AD^2 = 44

AD = √44

AD = 2√11

Итак, мы получаем, что AD равно 2√11.