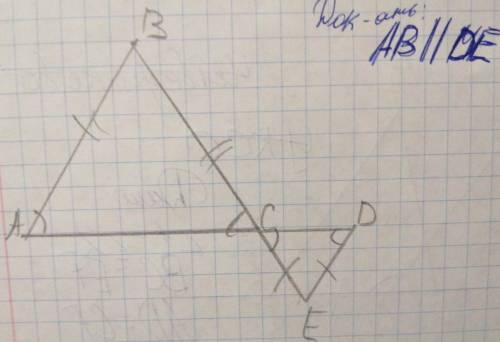
Треугольник ABC находится в треугольнике CDE секущая AD. Докажите что AB параллельно de

Чтобы доказать, что AB параллельно DE, мы можем использовать теорему о внутренних углах на пересекающихся прямых.

Теорема говорит следующее: если две прямые пересекаются третьей прямой, то каждая пара внутренних противоположных углов будет равна.

Обозначим точку пересечения AD и CE как F. Внутренний угол ABC, обозначенный как угол 1, будет равен внутреннему углу EDF, обозначенному как угол 2, по теореме о внутренних углах на пересекающихся прямых. Также, угол BCA, обозначенный как угол 3, будет равен углу FED, обозначенному как угол 4, также по теореме о внутренних углах на пересекающихся прямых.

Теперь нам нужно доказать, что углы 2 и 4 равны, чтобы показать, что AB параллельно DE. Для этого мы можем использовать другую теорему - теорему о соответствующих углах при пересечении параллельных прямых.

Теорема гласит: если две прямые параллельны, то соответствующие углы, образованные другой прямой, пересекающейся с ними, будут равны.

Из условия задачи нам известно, что AB находится в треугольнике CDE, а треугольник ABC находится в треугольнике CDE, поэтому AB и CD параллельны (по свойству вложенных треугольников). Следовательно, угол 1 и угол 2 должны быть равны, и угол 3 и угол 4 должны быть равны.

Таким образом, получаем, что углы 2 и 4 равны. Но угол 4 это угол BCA, а угол 2 это угол EDF. То есть, угол BCA равен углу EDF.

Таким образом, AB параллельно DE, т.к. углы BCA и EDF равны.

Это завершает доказательство.