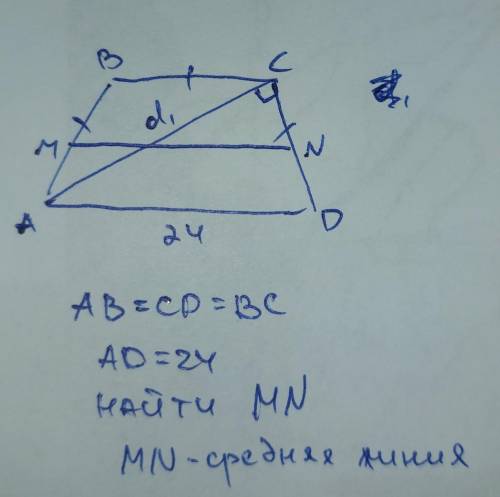
Трапеция. d1 образует с боковой стороной прямой угол, дано большое основание, меньшее основание и боковые стороны равны, надо найти среднюю линию :(
Другие вопросы по теме Геометрия
Популярные вопросы
- Кто такой вельможа и что он делал на службе у фараона?...
3 - Как составить памятку: как составить план....
2 - По учебник бененсон 1 класс 1часть стр.38 82 вопрос найди спрятавшиеся...
2 - Решить 2 . 50 ! (решение тоже нужно) 1.население города ежегодно...
1 - Температура воды при нормальном давлении 310 к кипит ли она?...
1 - 42*172+42*143+160*8=42( продолжите решение...
2 - Составь истинные высказывания: если из суммы вычесть одно слагаемое...
3 - Плохо знаю, болела сильно! про степени 1)2×2×2×5. 2)13×6×6×6×6 дальше...
1 - Написать сочинение на одну из трех тем. темы: 1) мои размышления...
2 - Разбить слоги и определить слоги открытый закрытый полузакрытый слог...
2
18
Объяснение:
Пусть АС = х, АВ = ВС = СD = у.
Так как сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение оснований трапеции, то для данной равнобедренной трапеции:
2х² = 2у²+ 2у ·24
или
х² - у² - 24у= 0 (1)
Так как:
х² = 24² - у²,
то перепишем (1) в виде:
24² - у² - у² - 24у = 0
-2у² - 24у + 576 = 0
у² + 12у - 288 = 0
у₁,₂ = - 6 ±√(36+288) = -6±√324 = -6±18
у = -6+18 = 12
Средняя линия:
(24 + 12) : 2 = 36 : 2 = 18
ответ: 18